Vermogensverdeling bij stroomtransport
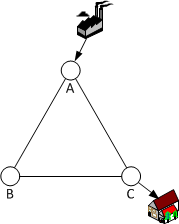
Voor het netwerk in figuur 1 is het de vraag hoe de stroom gaat lopen als de consument stroom afneemt. We leiden hier af dat de vermogensverdeling omgekeerd evenredig is aan de weerstandsverdeling van de mogelijke stroompaden.
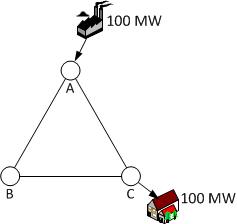
De eerste vraag is: hoeveel stroom neemt de consument bij C af? Laten we aannemen dat dat 100 MW is. Dat betekent dat er - als we de verliezen verwaarlozen - ook 100 MW moet worden opgewekt. Er is maar één centrale, dus de kolencentrale levert 100 MW, zie ook figuur 2.
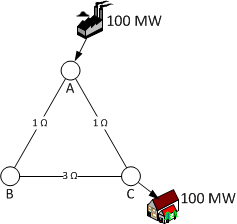
De energiebalans is nu gewaarborgd en daarmee is aan de eerste hoofdwet van de thermodynamica voldaan. Maar hoe gaan de stromen lopen? Om dat te kunnen berekenen moeten we de weerstanden van de routes weten. In het algemeen is de weerstand afhankelijk van de lengte en die bepaalt daarmee ook het netwerkverlies dat we voorlopig verwaarlozen. Laten we aannemen dat de lengtes niet gelijk zijn, zie figuur 3.
Laten we de wet van Ohm gebruiken per route om de stroom te transporteren van A naar C. Er zijn twee mogelijke routes, een directe route A-C en een tweede route via B (dus A-B-C).
De wet van Ohm zegt dus:
$$∆U_{AC} = I_{AC} R_{AC}$$
$$∆U_{ABC} = I_{ABC} R_{ABC}$$
Nu brengen we Kirchhoff's Spanningswet in beeld, welke zegt dat de potentiaalverschillen rondom een gesloten systeem 0 is. In andere woorden, als er meerdere routes zijn tussen A en C, dan zijn de potentiaalverschillen van alle routes gelijk.
Dat betekent in ons voorbeeld dat $∆U_{AC}$ gelijk is aan $∆U_{ABC}$. Door hiervan gebruik te maken, worden de twee eerder geformuleerde wetten van Ohm aan elkaar gelijk:
$$∆U_{AC} = ∆U_{ABC} = I_{AC} R_{AC} = I_{ABC} R_{ABC}$$
Dit betekent dat we het spanningsverlies niet hoeven te bepalen en dat we na omwerken meer weten over de verhouding van de stroomsterkte.
$${I_{AC}/I_{ABC}} = {R_{ABC}/R_{AC}}$$
We nemen nu ook aan dat het spanningsverlies verwaarloosbaar is ten opzichte van de spanning zelf. Door gebruik te maken van de wet van Joule wordt de verhouding tussen de vermogens over de verschillende routes $P$ gelijk aan de verhouding tussen de stroomsterktes $I$.
$${P_{AC}/P_{ABC}} = {I_{AC}/I_{ABC}} = {R_{ABC}/R_{AC}}$$
Voor ons voorbeeld wordt het dus:
$${P_{AC}/P_{ABC}} = {R_{ABC}/R_{AC}} = {4/1} = 4$$
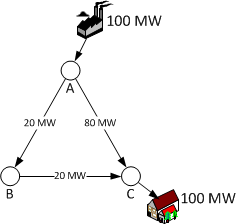
We weten dat het totaal van de routes gelijk is aan 100 MW, en daarmee kunnen we de vergelijking oplossen. Dit resultaat stelt dat het vermogen over route A-C 4 maal het vermogen is over route A-B-C, dus respectievelijk 80 MW en 20 MW.
Voor ingewikkeldere voorbeelden, waar de verhoudingen niet zo eenvoudig zijn te bepalen, is een alternatieve uitwerking mogelijk. Kirchhoff's Stroomsterktewet stelt dat in elke node de uitgaande stroom gelijk moet zijn aan de ingaande stroom. Voor node C geldt dus dat de 100 MW die wordt geconsumeerd (en de node uit gaat) ook binnenkomt. Daaruit volgt dat wat binnenkomt uit verbinding A-C en uit B-C samen 100 MW is. Aangezien B het vermogen slechts doorgeeft, blijkt uit dezelfde wet dat het vermogen A-B gelijk aan B-C, welke we eerder hebben gelabeld als $P_{ABC}$. In formulevorm betekent dit dus:
$$P_{AC} + P_{ABC} = 100$$
Omschrijven geeft $P_{ABC} = 100-P_{AC}$. Dit invullen in de vorige formule geeft:
$${P_{AC}/P_{ABC}} = {P_{AC}/(100-P_{AC})} = 4$$
Oplossen geeft:
$$P_{AC} = 4 (100-P_{AC}) = 400 - 4P_{AC} ⇒ 5P_{AC} = 400 ⇒ P_{AC} = 80$$
Uit $P_{AC} = 80$ MW volgt direct dat $P_{ABC} = 100 - 80 = 20$ MW
Hier hebben we dus afgeleid dat bij gelijkstroom, zonder verliezen, de volgende vuistregel geldt: Wanneer meerdere routes mogelijk zijn om stroom te transporteren van A naar B, worden de stroomsterkte en het vermogen verdeeld in een verhouding die omgekeerd evenredig is aan de weerstanden van elke route.
Laatste wijziging: 08-01-2024

Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.

Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.