Warmtewisselaars
In een warmtewisselaar wordt warmte van het ene fluïdum naar het andere getransporteerd. In kerncentrales wordt bijvoorbeeld warmte uit water dat in de buurt van de reactor is geweest, overgedragen naar water in een secundaire kringloop, waarmee vervolgens op een veiliger manier elektriciteit wordt opgewekt. In de voedingsmiddelenindustie worden producten opgewarmd of afgekoeld in warmtewisselaars. En in energiezuinige woningen wordt de warmte uit het wegstromende douchewater gebruikt om het binnenkomende water voor te verwarmen.
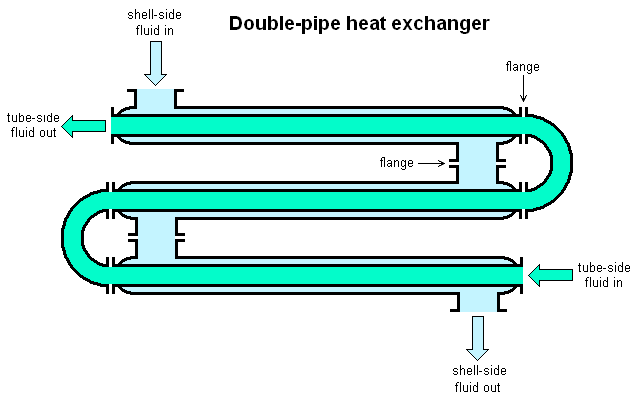
Figuur 1 laat een eenvoudige versie van de warmtewisselaar zien. Er zijn nog vele andere varianten - klik hier voor wat voorbeeldenw.
Aan een warmtewisselaar kunnen we in het kader van deze module rekenen met behulp van een balansvergelijking en een transportvergelijking.
Balansvergelijking
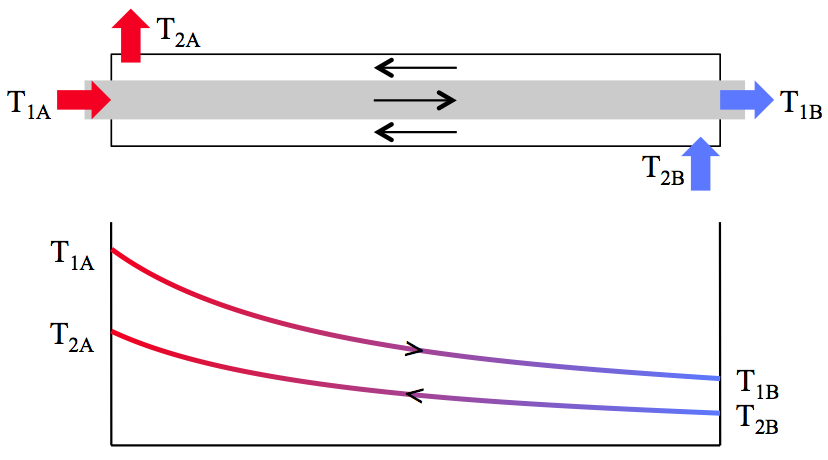
Onderstaande tekening geeft een warmtewisselaar in tegenstroom (zie verderop) schematisch weer, met daaronder de temperaturen als functie van de plaats. Fluïdum 1 stroomt daarin van links naar rechts, fluïdum 2 stroomt van rechts naar links.
Als deze warmtewisselaar in stationaire toestand werkt, is de warmte erbinnen constant. Dan geldt voor de warmtebalans dus:
$${dq}/{dt} = (φ_mc_p)_1(T_{1A} - T_{1B}) + (φ_mc_p)_2(T_{2B} - T_{2A}) = 0$$ Hierin geven subscripts "1" en "2" de verschillende fluïda aan, en "A" en "B" de beide uiteinden van de warmtewisselaar.
Transportvergelijking
De algemene vergelijking zou weer $φ_q = UA·ΔT$ kunnen zijn, maar er is een probleem: $ΔT$ is niet constant over de warmtewisselaar (zie de afbeeldingen). We moeten daarom eigenlijk de warmtestroom integreren tussen plaats A en plaats B. Die integratie valt buiten de inhoud van deze module, maar uiteraard hebben anderen het al gedaan, en kunnen we het resultaat gebruiken. De totale warmtestroom blijkt uit te drukken te zijn in het logaritmisch gemiddelde temperatuurverschil $ΔT_{lm}$, waarin "lm" staat voor "log mean":
$$ΔT_{lm} ={ΔT_A-ΔT_B}/{ln({ΔT_A}/{ΔT_B})}$$ Let er daarbij op dat "A" en "B" weer staan voor "uiteinde A" en "uiteinde B", niet voor de twee fluïda.
De warmtestroom is dan:
$$φ_q = UA·ΔT_{lm}$$
Meestroom, tegenstroom
Warmtewisselaars kunnen in mee- en in tegenstroom bedreven worden - zie figuren 3 en 4.
De vergelijkingen zijn voor beide gelijk, maar we moeten goed opletten naar welke locaties de temperaturen in de formules verwijzen.
Bij verder gelijke omstandigheden wordt in een warmtewisselaar in tegenstroom meer warmte overgedragen dan wanneer deze in meestroom gebruikt wordt.
Vraagstukken
Balans
Hoe verandert de balans als de warmtewisselaar in meestroom werkt?Curven 1
Waardoor wordt bepaald of de temperaturen in de warmtewisselaar verlopen zoals links of zoals rechts? ⬇ antwoord
Op iedere plaats in de warmtewisselaar geldt, dat de warmte die wordt overgedragen zorgt voor temperatuurdaling in het ene fluïdum en temperatuurstijging in de andere. Dus over een klein stukje lengte $ΔL$ van het apparaat geldt: $(φ_mc_pΔT)_1 = (φ_mc_pΔT)_2$. De grootste temperatuurverandering treedt dus op bij het fluïdum waar $φ_mc_p$ het kleinst is. In de linker afbeelding heeft het naar rechts stromende fluïdum dus de laagste waarde van $φ_mc_p$; in de rechter afbeelding geldt dit voor het naar links stromende fluïdum.
Curven 2
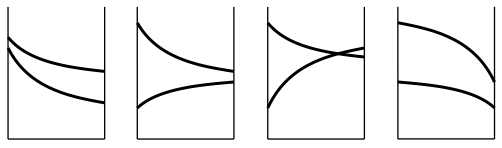
Leg van de onderstaande temperatuurcurven uit waarom ze wel of niet mogelijk zijn, en zo ja, of het dan om tegen- of meestroom gaat, en wat je dan kunt zeggen over de fysische eigenschappen van de fluïda. ⬇ antwoord
Van links naar rechts:
niet mogelijk — zie bijvoorbeeld het fluïdum met de laagste temperatuur: de snelste temperatuurverandering treedt op waar het temperatuurverschil het kleinst is; dit is niet mogelijk;
mogelijk — snelste temperatuurverandering waar het temperatuurverschil het grootst is; meestroom, want als het tegenstroom was, zou één van de fluïda opwarmen dan wel afkoelen tegen het temperatuurverschil in;
niet mogelijk — de temperaturen kunnen elkaar niet kruisen, want dan zouden de temperaturen daarna tegen het temperatuurverschil in veranderen;
niet mogelijk — om dezelfde reden als bij het meest linkse diagram.
niet mogelijk — zie bijvoorbeeld het fluïdum met de laagste temperatuur: de snelste temperatuurverandering treedt op waar het temperatuurverschil het kleinst is; dit is niet mogelijk;
mogelijk — snelste temperatuurverandering waar het temperatuurverschil het grootst is; meestroom, want als het tegenstroom was, zou één van de fluïda opwarmen dan wel afkoelen tegen het temperatuurverschil in;
niet mogelijk — de temperaturen kunnen elkaar niet kruisen, want dan zouden de temperaturen daarna tegen het temperatuurverschil in veranderen;
niet mogelijk — om dezelfde reden als bij het meest linkse diagram.
Olie
Olie met een $c_p$ van 2,0 kJ/kg/K stroomt door een tegenstroom-warmtewisselaar en wordt gekoeld van 394 K naar 339 K. Het debiet bedraagt 7,2 ton/uur. Het koelwater stijgt in temperatuur van 294 K naar 305 K. Het uitwisselend oppervlak A is 5,0 m². Hoeveel bedragen (a) het volumedebiet van het koelwater en (b) de totale warmteoverdrachtscoëfficiënt? ⬇ hint (a)
Dit volgt uit de warmtebalans.
⬇ antwoord (a)
Uit de balansvergelijking volgt dat $φ_mc_pΔT$ voor de olie is gelijk aan $φ_mc_pΔT$ voor het water ⇒ $φ_{m,w}$ = 17 ton/h.
⬇ hint (b)
Dit volgt uit de transportvergelijking, waarbij de overgedragen warmte ook gelijk moet zijn aan de warmte die de olie kwijtraakt, of het koelwater er bij krijgt.
⬇ antwoord (b)
Uit $φ_mc_pΔT = A·U·ΔT_{lm}$ en $ΔT_{lm}$ = (89-45)/ln(89/45) = 64,52°C volgt dan U = 0,69 kW/(m²K).
Koeling
Een reactiemengsel met een $c_p$ van 2,85 kJ/kg/K stroomt met een debiet van 2,0 kg/s en moet gekoeld worden van 105°C naar 70°C. Het beschikbare koelwater heeft een temperatuur van 15°C en een een debiet van 1,5 kg/s. De totale warmteoverdrachtscoëfficiënt U bedraagt 0,65 kW/(m²K).Bepaal (a) de uitlaattemperatuur van het water en (b) het benodigde oppervlak A voor (1) tegenstroom en (2) meestroom.
⬇ hint
Uit de warmtebalans volgt de temperatuurverandering van het water. A volgt dan uit $φ_mc_pΔT = UA·ΔT_{lm}$.
⬇ antwoord (a)
$φ_mc_pΔT$ voor het mengsel is gelijk aan $φ_mc_pΔT$ voor het water ⇒ de temperatuurstijging voor het water is 32°C, zodat de eindtemperatuur 47°C bedraagt.
⬇ antwoord (b)
(1)$ΔT_{lm}$ is bij tegenstroom (58-55)/ln(58/55) = 56,5°C, zodat uit $φ_mc_pΔT = UA·ΔT_{lm}$ volgt A = 5,4 m².
(2) Bij meestroom geldt $ΔT_{lm}$ = (90-23)/ln(90/23) = 49,1°C, zodat A = 6,3 m². Het benodigde oppervlak is bij meestroom dus groter dan bij tegenstroom.
(2) Bij meestroom geldt $ΔT_{lm}$ = (90-23)/ln(90/23) = 49,1°C, zodat A = 6,3 m². Het benodigde oppervlak is bij meestroom dus groter dan bij tegenstroom.
Tentamenvraagstuk
Glycerol (2) - Olijfolie - Warmtewisselaars - Water en stoomLaatste wijziging: 12-10-2022

Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.

Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.