Weergave van de resultaten van exergieanalyses
Er zijn verschillende manieren om de resultaten van exergieanalyses weer te geven, bijvoorbeeld grafisch in de vorm van Grassmann- of waardediagrammen of door het berekenen van rendementen.
Grassmann-diagram
Het Grassmann-diagram is het equivalent van het Sankey-diagram bij energieanalyses. De breedtes van de getekende stromen in het diagram zijn een maat voor de exergiewaarden van die stromen.
Waardediagram
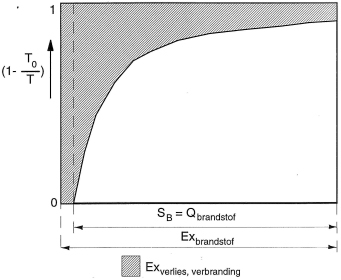
In een waardediagram worden de exergieverliezen zichtbaar gemaakt als oppervlaktes in het diagram. Op de horizontale as wordt de warmtehoeveelheid uitgezet en op de verticale as de bijbehorende temperatuur T in de vorm van 1-T0/T. De verticale as loopt van 0 tot 1.
Onderstaande figuur is een voorbeeld van een waardediagram. Het totale oppervlak van de figuur is gelijk aan de exergie-inhoud van de brandstof. Het oppervlak onder de afkoelkromme is gelijk aan de exergie-inhoud van de warmte die is vrijgekomen door de verbranding. Het gearceerde oppervlak is het exergieverlies veroorzaakt door de verbranding.
.
Universeel rendement
Het universele rendement is gedefinieerd als:
$$ η_{\Ex,\univ} = { \Σ Ex_{\uit,\j} } / { \Σ Ex_{\in,\i} } $$
met:
$Ex_{\in,\i}$ = exergie van ingaande proces- en energiestroom i
$Ex_{\uit,\j}$ = exergie van uitgaande proces- en energiestroom j
Het universele rendement heeft als nadeel dat de gevoeligheid van het rendement sterk afhangt van de grootte van de in- en uitgaande stromen, zoals behandeld bij de definities van rendementen.
Functioneel rendement
Bij het functionele rendement wordt onderscheid gemaakt tussen ‘essentiële’ en ‘ballast’stromen (Woudstra (1995)). Met ‘ballaststromen’ worden exergiestromen bedoeld die aan het proces toegevoerd worden maar niet direct betrokken zijn bij de beoogde omzetting. Het functionele rendement is gedefinieerd als:
$$ η_{\Ex,\func} = { \Σ Ex_{\product,\j} } / { \Σ Ex_{\bron,\i} } $$
met:
$Ex_{\bron,\i}$ = exergie van dat deel van ingaande proces- en energiestroom i dat bij het beschouwde proces als noodzakelijk voor het tot stand komen van het product kan worden aangemerkt
$Ex_{\product,\j}$ = exergie van dat deel van uitgaande proces- en energiestroom j dat als product van het systeem kan worden aangemerkt
Nadeel van het functionele rendement is dat er per systeem vastgesteld zal moeten worden welke stromen tot de product- en bronstromen behoren. Door Woudstra (1995) is dit voor een groot aantal apparaten gedaan, waaronder voor turbines, condensors, pompen, warmtewisselaars, compressoren. Het functionele exergierendement van een warmtewisselaar is bijvoorbeeld gedefinieerd als de exergie opgenomen door de opwarmende stroom gedeeld door de exergie afgegeven door de afkoelende stroom. In formulevorm:
$$ η_{\Ex,\func,\ww} = { Ex_{\opwarmende \stroom, \uit} - Ex_{\opwarmende \stroom, \in} } / { Ex_{\afkoelende \stroom,\in} - Ex_{\afkoelende \stroom,\uit} } $$
Bronnen
Stougie et al. (1997), Stougie, L., G. C. J. Bart, H. J. van der Kooi, H. van der Ree, N. Woudstra en T. Woudstra (1997). Syllabus Exergie-analyse, TU Delft, InterductWoudstra (1995), Woudstra, N. (1995). Exergetische rendementen, TU Delft
Laatste wijziging: 12-10-2022

Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.

Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.