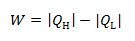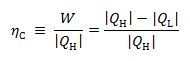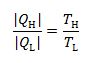Processen in de energiesector
Deze website vormt het webdictaat voor het vak TB242E Processen in de energiesector, behorende bij de opleiding Technische Bestuurskunde aan de TU Delft, in het collegejaar 2024-2025. Dit webdictaat kan het beste worden bekeken met de browsers Chrome, Safari en evt. (afhankelijk van het besturingssysteem) ook Firefox.
Het dictaat kan op meerdere manieren worden bestudeerd:
• per college: in het menu links staat een overzicht van het dictaat ingedeeld per college. Voor elk college staat daar een link naar de beginpagina van dat college en een overzicht met de pagina's van het webdictaat die relevant zijn voor het betreffende college.
• alles op één pagina: er is een printbare versie waarin alle pagina's in collegevolgorde zijn opgenomen.
• naar eigen inzicht: links in het menu is een zoekfunctie.
• ook kan er een overzicht (in bewerking) met de belangrijkste formules worden gegenereerd.
Voor contactinformatie en referenties, zie het colofon.
Voor meer informatie over dit vak:
Brightspacew
Studiegidsw
Op- en aanmerkingen zijn van harte welkom: l.stougie@tudelft.nl.
Heel veel plezier en succes met het bestuderen van het webdictaat.
Met vriendelijke groet,
Lydia Stougie, modulemanager.
Colofon
Auteur
dr.ir. Lydia Stougie, l.stougie@tudelft.nl
Copyright © 2024 TU Delft, L. Stougie. Tenzij anders vermeld is alles in deze publicatie gelicenseerd onder een Creative Commons Naamsvermelding GelijkDelen 4.0. Kijk op deze licentiepaginaw voor een volledige tekst van de licentie.

Refereren
Algemene referentie:Stougie, L. (2024) Webdictaat Processen in de energiesector, http://eduweb.eeni.tbm.tudelft.nl/TB242E.
Referentie naar een specifieke pagina:
Paginatitel, in: Stougie, L. (2024) Webdictaat Processen in de energiesector, http://eduweb.eeni.tbm.tudelft.nl/TB242E/pagina.
Disclaimer
Hoewel de auteur van dit webdictaat de uiterste zorgvuldigheid heeft betracht, aanvaarden de auteurs en de uitgever geen enkele aansprakelijkheid voor eventuele fouten en onvolkomenheden, noch voor de gevolgen daarvan.Pagina’s in college-volgorde
In onderstaande tabel staan de beginpagina's voor elk college:
| Week | maandag | dinsdag | woensdag | donderdag | vrijdag |
| 1 | Introductie thermodynamica | Idem (vervolg) | |||
| 2 | Fasediagrammen | Toestandsdiagrammen | |||
| 3 | Kringprocessen | Idem (vervolg) | |||
| 4 | Elektriciteitscentrales | Werkcollege | |||
| 5 | Onderdelen van elektriciteitscentrales | Werkcollege | |||
| 6 | Warmtepompen | Werkcollege | |||
| 7 | Brandstofcellen en elektrolyse | Werkcollege | |||
| 8 | Exergieanalyse | Werkcollege | |||
| 9 | Zonne-energie | Vragencollege | |||
| 10 | Tentamen |
De diverse pagina's zijn onderling sterk verbonden. Om zeker te weten welke pagina's bij welk college horen, staat hieronder een weekindeling van alle pagina's. Bij een aantal onderwerpen wordt achtergrondinformatie gegeven. Deze informatie hoeft niet bestudeerd te worden (het is immers achtergrondinformatie), maar het kan uiteraard wel handig/interessant zijn bij de voorbereiding op het tentamen.
Week 1: Introductie thermodynamica
thermodynamica-introductietoestandsgrootheden-introductie
toestandsgrootheden-faseregel
toestandsgrootheden-invloed-pT
Week 1: Introductie thermodynamica (vervolg)
toestandsgrootheden-mengselstoestandsvergelijkingen
eerste-hoofdwet-toepassen
Week 2: Fasediagrammen
fasediagrammen-introductiefasediagrammen-kritisch
fasediagrammen-Tx
tweefasesystemen-toestandsgrootheden
tweefasesystemen-wet-van-Raoult
Week 2: Toestandsdiagrammen
toestandsdiagrammentoestandsveranderingen-berekeningen
Week 3: Kringprocessen
kringprocessen-introductiekringprocessen-Carnot
Week 3: Kringprocessen (vervolg)
kringprocessen-Rankinekringprocessen-Brayton
Week 4: Elektriciteitscentrales
elektriciteitscentrales-soortenelektriciteitscentrales-rendementen
elektriciteitscentrales-regelbaarheid
Week 5: Onderdelen van elektriciteitscentrales
elektriciteitscentrales-onderdelenWeek 6: Warmtepompen
warmtepompenpinch-analyse
Week 7: Brandstofcellen en elektrolyse
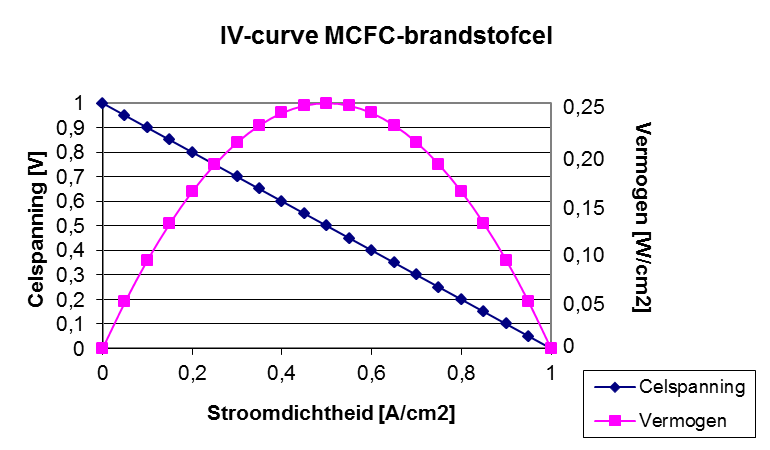
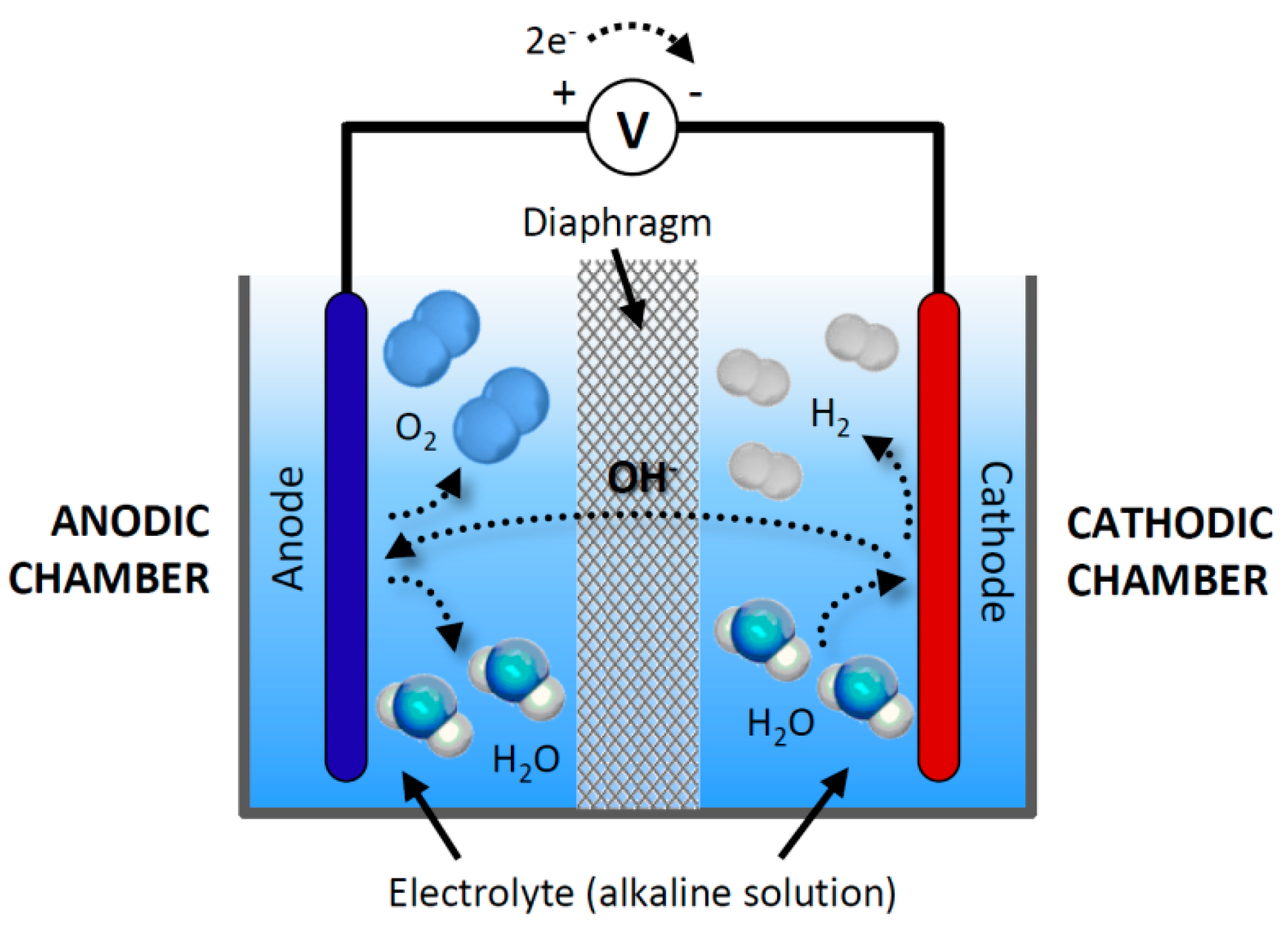
brandstofcellenelektrolyse
Week 8: Exergieanalyse
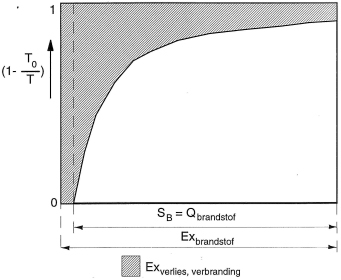
exergie-introductieexergieverlies
exergieverlies-oorzaken
exergiewaarden-berekening
exergieanalyse-resultaten
Week 9: Zonne-energie
zonne-energiekringprocessen-Stirling
Introductie thermodynamica
Wat is thermodynamica?
De thermodynamica houdt zich bezig met allerlei soorten energieomzettingen en is ontstaan in de tijd dat men zich bezighield met de omzetting van warmte in kracht. Het woord thermodynamica is dan ook afkomstig van de Griekse woorden ‘therme’ (warmte) en ‘dynamis’ (kracht). Thermodynamica wordt gebruikt bij de analyse en het ontwerp van apparaten. Voor meer informatie over thermodynamica wordt verwezen naar de basisboeken thermodynamica, bijvoorbeeld die geschreven door Moran & Shapiro en Smith & Van Ness. Deze boeken zijn ook gebruikt als naslagwerk bij het schrijven van dit webdictaat.
Hoofdwetten
De thermodynamica kent een aantal hoofdwetten. Deze hoofdwetten zijn gebaseerd op ervaring en worden gebruikt bij thermodynamische berekeningen. De wet van behoud van energie wordt ook wel de eerste hoofdwet genoemd, maar feitelijk is de eerste hoofdwet gebaseerd op de wet van behoud van energie. Volgens de wet van behoud van energie geldt: energie kan niet uit het niets ontstaan en ook niet verloren gaan. Bij het toepassen van deze (hoofd)wet wordt onderscheid gemaakt tussen het beschouwde systeem en zijn omgeving. Voor systeem en omgeving samen geldt:
$$ \Δ(\energie \van \het \systeem) + \Δ(\energie \van \de \omgeving) = 0 $$
De eerste hoofdwet kan worden toegepast op gesloten en open systemen.
De tweede hoofdwet heeft te maken met de richting van energieomzettingen. Zo zal warmte van warme naar koude voorwerpen stromen en niet andersom. Een andere formulering van de tweede hoofdwet is dat het onmogelijk is om met een cyclisch proces de warmte die door een systeem geabsorbeerd wordt volledig in arbeid om te zetten. De tweede hoofdwet stelt verder dat een proces alleen in een zodanige richting kan verlopen dat de totale entropieverandering veroorzaakt door dat proces groter is dan of gelijk is aan nul. Entropie is een voorbeeld van een toestandsgrootheid en kan beschouwd worden als ‘wanorde’. Met totale entropieverandering wordt de entropieverandering van systeem en omgeving samen bedoeld, in formulevorm:
$$ \ΔS_\totaal = \ΔS_\systeem + \ΔS_\omgeving ≥ 0 $$
In werkelijkheid is de entropieverandering altijd groter dan nul. Alleen bij denkbeeldige processen die omkeerbaar verlopen is de entropieverandering gelijk aan nul. Deze denkbeeldige processen worden reversibele processen genoemd.
De nulde hoofdwet is fundamenteler dan de eerste en tweede hoofdwetten, maar werd later geformuleerd en is daarom de nulde hoofdwet genoemd. Deze nulde hoofdwet stelt dat wanneer twee systemen in thermisch evenwicht zijn met een derde systeem (= dezelfde temperatuur hebben), zij ook in thermisch evenwicht met elkaar zijn.
De derde hoofdwet heeft te maken met het absolute nulpunt van de temperatuur, -273,15 °C. Bij dat absolute nulpunt zijn moleculen bewegingloos en is er geen onduidelijkheid meer over waar moleculen zich bevinden, m.a.w. er is geen wanorde meer. De formulering van de derde hoofdwet van de thermodynamica is dan ook: de entropie van een zuivere kristallijne stof bij het absolute nulpunt is nul.
Introductie toestandsgrootheden
Wat is een toestandsgrootheid?
In de thermodynamica wordt onderscheid gemaakt tussen twee soorten grootheden (een grootheid is iets wat je kunt meten), namelijk grootheden die padafhankelijk zijn, d.w.z. afhankelijk zijn van de afgelegde weg die geleid heeft tot de huidige toestand van een stof, en grootheden die dat niet zijn. Een toestandsgrootheid is onafhankelijk van de afgelegde weg en is een macroscopisch kenmerk van een stof of systeem. Er wordt dus niet naar de kenmerken van de afzonderlijke moleculen gekeken.
Toestandsgrootheden zijn dus alleen afhankelijk van de omstandigheden op dat moment, zoals druk en temperatuur en de samenstelling. Voorbeelden van toestandsgrootheden zijn druk, temperatuur en specifiek volume. Het specifieke volume is het volume van een stof per hoeveelheid van die stof. Andere voorbeelden van toestandsgrootheden zijn: inwendige energie, entropie, enthalpie, Gibbs energie en Helmholtz-energie.
Inwendige energie
De inwendige energie (symbool: U) van een stof is de energie die een stof heeft doordat de moleculen waaruit die stof bestaat een hoeveelheid energie vertegenwoordigen. Deze moleculen bezitten bijvoorbeeld energie in de vorm van rotatie- en translatie- en vibratie-energie en potentiële energie door de interacties tussen moleculen en de bindingen tussen de atomen van deze moleculen. De absolute waarde van de inwendige energie van stoffen is onbekend, maar dat is geen probleem doordat in de thermodynamica alleen de verandering in inwendige energie van belang is.
Entropie
Entropie (symbool: S) is een abstracter begrip. De entropie van een stof kan gezien worden als een maat voor de moleculaire wanorde van die stof. Doordat de moleculen van een stof in de gasfase vrijer kunnen bewegen dan de moleculen van dezelfde stof in de vloeistoffase, is de wanorde van de stof in de gasfase groter. De entropie van een stof in de gasfase is dus groter dan de entropie van een stof in een vloeistoffase en die is op zijn beurt weer groter dan die van een stof in de vaste fase.
Enthalpie
De enthalpie (symbool: H) van een stof is geïntroduceerd omdat het een handige grootheid is om te gebruiken bij thermodynamische analyses, vooral bij stoomturbines. Bij open systemen komt de combinatie van inwendige energie (U) en stromingsarbeid (pV) namelijk veel voor, wat geleid heeft tot de volgende definitie van de enthalpie van een stof:
$$ H ≡ U + pV $$
met:
$U$ = inwendige energie
$p$ = absolute druk
$V$ = volume
Als de ΔH van een proces, dus Heind – Hbegin, groter is dan nul dan betekent dit dat er warmte toegevoerd moet worden. Het proces is endotherm. In het tegengestelde geval is het proces exotherm, er moet warmte afgevoerd worden.
Gibbs energie en Helmholtz-energie
De afgeleide toestandsgrootheden Gibbs energie (symbool: G) en Helmholtz-energie (symbool: A of F) zijn ook geïntroduceerd omdat dit handige toestandsgrootheden zijn om mee te werken:
$$ G ≡ H - TS $$
$$ A ≡ U - TS $$
De Gibbs energie wordt gebruikt voor processen bij constante p en T en de Helmholtz-energie voor processen bij constante V en T. De absolute waarde van een negatieve waarde voor de ΔG of ΔA van zo'n proces is gelijk aan de maximale hoeveelheid arbeid die dat proces kan leveren. NB: Dit is een andere vorm van arbeid dan de volumearbeid, aangeduid met symbool W, die een rol speelt bij toestandsveranderingen.
Intensieve en extensieve toestandsgrootheden
De druk en temperatuur van een stof zijn onafhankelijk van de hoeveelheid van die stof. Deze toestandsgrootheden worden intensieve grootheden genoemd. De inwendige energie en het volume van een stof zijn wel afhankelijk van de hoeveelheid en worden extensieve grootheden genoemd. Bij de specifieke (waarde per kg) en molaire (waarde per mol) varianten van inwendige energie en volume is de hoeveelheid niet meer van belang; dit zijn dus ook intensieve grootheden.
In principe worden de intensieve toestandsgrootheden met een hoofdletter aangeduid als het om de absolute waarde gaat (bijv. H, met als eenheid J) en met een kleine letter als het om de specifieke of molaire waarde gaat (bijv. h, met als eenheid J/kg of J/mol). Deze regel wordt niet altijd toegepast, maar vaak blijkt ook uit de context of eenheid van de toestandsgrootheid of het om de absolute of specifieke/molaire waarde gaat.
Volgens de faseregel van Gibbs kunnen de intensieve toestandsgrootheden niet allemaal onafhankelijk van elkaar vastgelegd worden.
Achtergrondinformatie
• Youtube-filmpje over entropiew (gaat ook in op verband G, H en S, een aanrader!)
• dossier entropiew (entropie uitgelegd vanuit microscopische invalshoek plus hoofdwetten van de thermodynamica)
Faseregel van Gibbs
Voor een homogene zuivere stof geldt dat de thermodynamische toestand vastligt op het moment dat twee intensieve toestandsgrootheden vastliggen of op een bepaalde waarde worden gehouden. Homogeen wil zeggen dat de stof zich in één fase bevindt, dus of volledig vast, of volledig vloeibaar of volledig gasvormig is. Wanneer er sprake is van meerdere fases is de stof heterogeen. Wanneer bijvoorbeeld de druk en temperatuur van een zuiver gas bekend zijn, ligt ook de dichtheid van dat gas vast.
Wanneer er sprake is van twee fases, bijvoorbeeld een kokende vloeistof, ligt bij een bepaalde druk ook de temperatuur vast. Er is dan nog niet bekend welk deel van de stof gasvormig is en welk deel vloeibaar. De intensieve thermodynamische toestand van een stof in evenwicht ligt vast op het moment dat de temperatuur, druk en de samenstelling van alle fases vastliggen. Het aantal intensieve toestandsgrootheden dat hierbij onafhankelijk van elkaar vastgelegd kan worden, volgt uit de faseregel van Gibbs. Voor niet-reagerende systemen is deze faseregel als volgt:
$$ F = 2 - π + N $$
met:
$F$ = aantal vrijheidsgraden (het aantal intensieve toestandsgrootheden dat onafhankelijk van elkaar vastgelegd kan worden)
$π$ = aantal fases
$N$ = aantal chemische stoffen
Het verband tussen druk, temperatuur en volume van een stof kan worden beschreven door middel van toestandsvergelijkingen en kan worden weergegeven in fasediagrammen.
Invloed van druk en temperatuur op toestandsgrootheden
Bij processen waarbij de druk niet verandert (bijvoorbeeld bij een stationair proces met een in- en uitgaande stroom waarbij uitsluitend warmteuitwisseling tussen systeem en omgeving plaatsvindt) of waarbij de enthalpie van de stof onafhankelijk is van de druk, geldt:
$$ \ΔH = C_\p\ΔT $$
waarin Cp de warmtecapaciteit bij constante druk is. De enthalpie van een stof is onafhankelijk van de druk bij ideale gassen en bij benadering bij gassen bij lage druk, bij vaste stoffen en bij vloeistoffen buiten het kritische gebied. De warmtecapaciteit per hoeveelheid massa wordt de specifieke warmtecapaciteit of soortelijke warmte genoemd en wordt aangeduid met een kleine letter c. De cp van een stof is de hoeveelheid warmte die nodig is om 1 kg van de betreffende stof 1 graad (°C of K) in temperatuur te laten stijgen bij constante druk. Er geldt dus:
$$ C_\p = m ⋅ c_\p $$
Aangezien de Cp afhankelijk is van de temperatuur is het beter om met de gemiddelde Cp voor enthalpieberekeningen te rekenen:
$$ \ΔH = C_{\p,\mh}\ΔT $$
Bij processen waarbij het volume constant is (bijvoorbeeld bij een gesloten systeem waarbij uitsluitend warmteuitwisseling tussen systeem en omgeving optreedt) of waarbij de inwendige energie van de stof onafhankelijk is van het volume, geldt:
$$ \ΔU = C_\V\ΔT $$
waarin CV de warmtecapaciteit bij constant volume is. De inwendige energie is onafhankelijk van het volume bij ideale gassen en niet-comprimeerbare vloeistoffen.
De entropie van een stof is zowel afhankelijk van de temperatuur als van de druk. Voor een stof die zich gedraagt als een ideaal gas geldt er (per mol van de stof):
$$ \ΔS^\ig = c_{\p,\ms}^\ig \ln({T_{\eind}}/{T_{\begin}}) - R \ln({p_{\eind}}/{p_{\begin}}) $$
met:
$c_{\p,\ms}^\ig$ = gemiddelde cp van een ideaal gas voor entropieberekeningen.
NB: bij ongeveer constante temperatuur kan de betreffende $c_{\p}^\ig$ gebruikt worden
De $c_{\p,\ms}^\ig$ van een stof kan als volgt berekend worden (voor het vak TB242E hoeft deze formule niet uit het hoofd geleerd te worden):
$$ c_{\p,\ms}^\ig / R = A + B ⋅ T_{\lm} + T_{\am}T_{\lm}(C + D/(T_{\begin} ⋅ T_{\eind})^2) $$
met:
$A$, $B$, $C$, $D$ = stofconstantes voor de betreffende stof zoals deze in algemene thermodynamische (tabellen)boeken te vinden zijn
$T_{\am}$ = arithmic mean, rekenkundig gemiddelde temperatuur
$T_{\lm}$ = logarithmic mean, logaritmisch gemiddelde temperatuur
$T_{\lm}$ staat ook bekend als de thermodynamisch gemiddelde temperatuur en wordt als volgt berekend:
$$ T_{\lm} = { T_{\eind} - T_{\begin} } / { \ln({ T_{\eind} } / { T_{\begin} } )} $$
Bovenstaande formules kunnen gebruikt worden om de waardes van toestandsgrootheden te berekenen bij andere temperaturen en drukken dat de standaardtemperatuur en -druk. Aangezien geldt dat:
$$ G = H - TS $$
kan de verandering in Gibbs energie bij een constante temperatuur, die dus een andere temperatuur kan zijn dan T0, berekend worden uit de veranderingen in enthalpie en entropie bij die temperatuur volgens:
$$ \ΔG = \ΔH - T\ΔS $$
Toestandsgrootheden van mengsels
De toestandsgrootheden van mengsels worden berekend op basis van de molfracties van de verschillende componenten van het mengsel en de waarde van de toestandsgrootheid voor die component. De molfractie van een component is het aantal mol van die component gedeeld door het totaal aantal mol.
Gasmengsels hebben gewoonlijk een hoge temperatuur en lage druk ten opzichte van de temperatuur en druk van het kritische punt van de individuele gassen. In dat geval kan aangenomen worden dat het mengsel en de componenten zich gedragen als ideale gassen, d.w.z. dat de moleculen geen volume hebben en er geen interacties zijn tussen de moleculen. Er geldt dan:
$$ nM^{ig}(T,p) = \Σ(n_kM_k^\ig(T,p_k)) $$
met:
$M$ = $A$, $G$, $H$, $S$, $U$ of $C_\p$
$n_k$ = aantal mol van component k
$p_k$ = partiaaldruk van component k
Aangezien $H$, evenals $U$ en $C_\p$, onafhankelijk van de druk is, geldt er (na delen door $n$) voor $h^{\ig}$:
$$ h^\ig = \Σ(y_kh_k^\ig) $$
Voor de entropie van een ideaal gas (die wel afhankelijk van de druk is) geldt:
$$ s^\ig = \Σ(y_ks_k^\ig) - \R \Σ(y_k\ln(y_k)) $$
Het verschil tussen de berekening van de enthalpie en entropie van een mengsel is dat in het laatste geval een mengterm benodigd is:
$$ Δs_{mix} = - \R \Σ(y_k\ln(y_k)) $$
En met:
$$ G^\ig = H^\ig - TS^\ig $$
volgt uit het bovenstaande dat geldt:
$$ g^\ig = \Σ(y_kg_k^\ig) + RT \Σ(y_k\ln(y_k)) $$
Analoog aan de enthalpie kan de soortelijke warmte van een ideaal gasmengsel berekend worden uit de soortelijke warmte van de individuele gassen en hun molfracties:
$$ c^{\ig}_{\p,\mengsel} = \Σ(y_\i ⋅ c^{\ig}_{\p,\i}) $$
met:
$y_{\i}$ = molfractie van component i [-]
$c_{\p,\mh,\i}$ = soortelijke warmte van component i [J/(mol⋅K)]
Als de eenheid van soortelijke warmte [J/kgK] is dan dienen uiteraard massa- ipv molfracties gebruikt te worden om de soortelijke warmte van het mengsel te berekenen.
Oplossingen die bestaan uit moleculen van dezelfde grootte en waarbij de krachten tussen de moleculen gelijk zijn, gedragen zich ideaal. Dit geldt bij benadering voor moleculen die niet teveel verschillen in grootte en van dezelfde chemische soort zijn, bijvoorbeeld een mengsel van isomeren zoals ortho-, meta- en para-xyleen en een mengsel van ethanol en propanol. Aangezien het bij oplossingen vaak om vloeistoffen gaat, wordt de molfractie aangeduid met x. De vergelijkingen voor het berekenen van de enthalpie, entropie, Gibbs energie en soortelijke warmte van ideale vloeistofmengsels zijn vergelijkbaar met de vergelijkingen voor ideale gasmengsels. Er geldt:
$$ h^{\i\d} = \Σ(x_ih_i) $$
$$ s^{\i\d} = \Σ(x_is_i) - R \Σ(x_i\ln(x_i)) $$
$$ g^{\i\d} = \Σ(x_ig_i) + RT \Σ(x_i\ln(x_i)) $$
$$ c^{\i\d}_{\p,\mh,\mengsel} = \Σ(x_\i ⋅ c^{\i\d}_{\p,\mh,\i}) $$
Toestandsvergelijkingen
Vergelijkingen die het verband tussen de temperatuur, druk en het specifieke volume van een stof beschrijven, worden toestandsvergelijkingen genoemd. Ook vergelijkingen met andere eigenschappen van een stof in evenwicht worden toestandsvergelijkingen genoemd.
Ideaal gaswet
De vergelijking voor een ideaal gas is de bekendste toestandsvergelijking:
$$ pV = nRT $$
met:
$p$ = absolute druk [Pa]
$V$ = volume [m3]
$n$ = aantal mol van de stof [mol]
$R$ = universele gasconstante [8,314 J/molK]
$T$ = absolute temperatuur [K]
De toestandsvergelijking voor een ideaal gas kan ook gebruikt worden voor niet-ideale gassen die een lage dichtheid hebben, dus bij lage drukken en hoge temperaturen. Bekende gassen zoals lucht, stikstof, zuurstof, waterstof en kooldioxide gedragen zich ongeveer als een ideaal gas bij atmosferische druk in de buurt van kamertemperatuur.
Toestandsvergelijking reëel gas
Het gedrag van een reëel gas kan benaderd worden met de vergelijking:
$$ pv = ZRT $$
met:
$v$ = molair volume [m3/mol] (= $V$/$n$)
$Z$ = $v_{\reë\el}$/$v_{\ideaal}$ = compressibiliteitsfactor
Voor een ideaal gas is Z gelijk aan 1, voor een reëel gas is Z kleiner dan 1, gelijk aan 1 of groter dan 1. In 1873 realiseerde de Nederlandse natuurkundige Johannes Diderik van der Waalsw zich als eerste dat Z ongeveer hetzelfde is voor alle gassen bij een bepaalde pR (gereduceerde druk) en TR (gereduceerde temperatuur). De gereduceerde druk en temperatuur zijn gelijk aan respectievelijk de druk gedeeld door de kritische druk en de temperatuur gedeeld door de kritische temperatuur.
Toestandsvergelijking Van der Waals
Van der Waals heeft de ideaal-gasvergelijking uitgebreid door in zijn vergelijking ook de wederzijdse aantrekkingskracht tussen de moleculen en het volume dat door de moleculen zelf wordt ingenomen, mee te nemen:
$$ (p + {n^2a} / {V^2})(V - nb) = nRT $$
De drukcorrectieterm ‘n2a/V2’ verdisconteert de aantrekking tussen de moleculen en de volumecorrectieterm ‘nb’ het volume van de moleculen. De waardes van a en b verschillen per stof. De geldigheid van deze vergelijking voor de beschrijving van reële gassen en vloeistoffen is beperkt en de vergelijking is niet goed toepasbaar bij drukken en temperaturen waarbij damp en vloeistof met elkaar in evenwicht zijn (het tweefasegebied).
Andere toestandsvergelijkingen
Na de Van der Waalsvergelijking zijn er nog vele andere toestandsvergelijkingen bedacht die het ‘gedrag’ van een gas of vloeistof beschrijven. Bijvoorbeeld de viriaal-vergelijking:
$$ {pv} / {RT} = 1 + {B} / {v} + {C} / {v^2} + {D} / {v^3} + … $$
met:
$B$, $C$, $D$, … = resp. tweede, derde, vierde etc viriaalcoëfficiënt
Normaal- en standaardcondities
Bij volumeberekeningen met behulp van toestandsvergelijkingen wordt vaak gebruik gemaakt van algemeen bekende waardes voor druk en temperatuur. Bijvoorbeeld normaalcondities, ofwel 1 atm en 0 °C, bij de berekening van gasvolumes. Het volume wordt in dat geval uitgedrukt in Nm3, waarbij de 'N' staat voor 'normaal'. Bij de berekening van toestandsgrootheden wordt vaak uitgegaan van een standaardtoestand van 1 atm en 25 °C.
Voorbeelden van andere standaarden zijn NIST (National Institute of Standards and Technology), namelijk 1 atm en 20 °C, en de STP (standard temperature and pressure) van de IUPAC (International Union of Pure and Applied Chemistry), namelijk 1 bar en 0 °C, voor scheikundige berekeningen.
Achtergrondinformatie
• gaswettenw (ideaal gaswet, wet van Boyle etc)
• reële gassenw (oorzaken niet-ideaal gedrag, compressibiliteitsfactor)
Toepassing eerste hoofdwet op gesloten en open systemen
Er is sprake van een gesloten systeem wanneer er geen uitwisseling is van massastromen tussen het systeem en de omgeving. Dit wil niet zeggen dat er bij een gesloten systeem helemaal geen uitwisseling tussen systeem en omgeving plaatsvindt, want uitwisseling van warmte en/of arbeid tussen systeem en omgeving is nog wel mogelijk.
Er zijn verschillen tussen scheikundigen en natuurkundigen wat betreft het positief of negatief rekenen van de uitwisseling van warmte en arbeid tussen systeem en omgeving. In dit webdictaat wordt aangesloten bij wat gebruikelijk is bij de bestudering van warmtemotoren, namelijk dat de warmte die vanuit de omgeving aan een systeem toegevoerd wordt een positief teken heeft (een positieve waarde heeft) en dat de arbeid die een systeem levert ook een positief teken heeft, zie onderstaande tabel met tekenafspraken m.b.t. warmte en arbeid.
| Toegevoerd aan systeem | Geleverd door systeem | |
| warmte | + | - |
| arbeid | - | + |
Volgens de wet van behoud van energie is de totale hoeveelheid energie altijd constant, dus op het moment dat de energie van het systeem toeneemt, neemt de hoeveelheid energie van de omgeving af. Onder de aanname dat de andere vormen van energie, zoals kinetische, potentiële en magnetische energie geen rol spelen, geldt dat de energieverandering van het systeem gelijk is aan de verandering in inwendige energie van het systeem. Bij een gesloten systeem is de energieverandering van de omgeving gelijk aan de hoeveelheid energie die uitgewisseld wordt met het systeem in de vorm van warmte en/of arbeid die de systeemgrens passeert.
De hoeveelheid inwendige energie neemt toe wanneer er een hoeveelheid warmte wordt toegevoerd vanuit de omgeving naar het systeem en neemt af wanneer het systeem arbeid levert. Hiermee wordt de eerste hoofdwet voor een gesloten systeem:
$$ \ΔU = Q - W $$
Wanneer er wel uitwisseling van massastromen tussen systeem en omgeving plaatsvindt, is niet de verandering in inwendige energie maar de verandering in enthalpie van belang. Analoog aan bovenstaande vergelijking geldt voor de eerste hoofdwet voor een stationair open systeem met een toe- en een afvoerstroom:
$$ \ΔH = Q - W $$
Hierbij wordt met $W$ de arbeid exclusief de stromingsarbeid bedoeld, aangezien de stromingsarbeid al wordt meegenomen in de enthalpiewaarden.
Fasediagrammen
Zoals de naam al doet vermoeden, worden in een fasediagram de verschillende fases van een stof weergegeven. Gebruikelijke fasediagrammen zijn het p,T-diagram en het p,V-diagram. Een Tx-diagram wordt gebruikt bij mengsels van stoffen.
p,T-diagram
In het p,T-diagram geven de curven twee-fasegebieden aan. De getrokken groene curve (= de bovenste getrokken curve) in onderstaande figuur geeft het vriespunt voor de meeste stoffen als functie van de druk weer; de gestreepte groene curve is van toepassing op water. De blauwe curve (= de curve tussen ‘triple point’ en ‘critical point’) geeft het kookpunt als functie van de druk aan.
(*) De getrokken (groene) curve tussen 'solid phase' en 'liquid phase/compressible liquid' zou vanaf het triple punt eigenlijk bijna loodrecht omhoog moeten beginnen en vervolgens boven de kritische druk moeten afbuigen in de richting van toenemende temperatuur.
p,V-diagram
In het p,V-diagram worden de twee-fasegebieden aangegeven met vlakken. Het p,V-diagram in onderstaande figuur geldt voor een stof waarvan verondersteld wordt dat het volume onafhankelijk is van de druk.
p,V-diagram van een stof waarbij het volume onafhankelijk van de druk is verondersteld (*). (bron: S.B.A. Inventw)
(*) De curve tussen de gebieden 'Solid + Vapor' en 'Vapor' zou vanaf de druk bij het triple punt eigenlijk minder steil naar beneden moeten gaan.
Isobaar, isotherm en isochoor
In fase- en toestandsdiagrammen worden vaak isobaren, isothermen en isochoren getekend. De termen isobaar, isotherm en isochoor betekenen dat respectievelijk de druk, de temperatuur en het volume constant zijn tijdens het betreffende proces.
Achtergrondinformatie
• fasediagrammenw (tekenen en interpreteren van eenvoudige p,T-diagrammen)
• vast/vloeistof-fasediagrammenw (tekenen van fasediagrammen toegepast op vast/vloeistofsystemen)
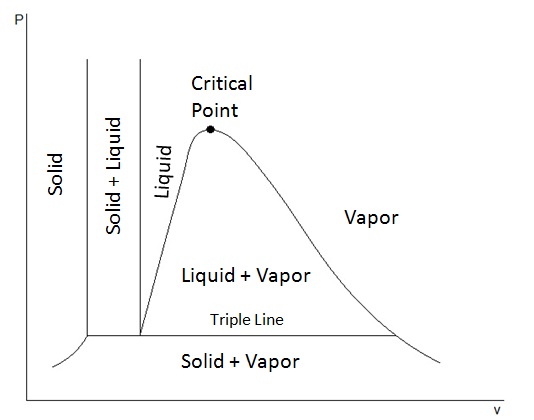
Kritische druk, kritische temperatuur en superkritisch gedrag
In fasediagrammen is er sprake van een kritisch punt. Dit kritische punt bevindt zich bij een bepaalde druk, de kritische druk (pc), en bij een bepaalde temperatuur, de kritische temperatuur (Tc). Wanneer de druk en temperatuur van een stof hoger zijn dan de kritische druk en kritische temperatuur van die stof, vertoont deze stof superkritisch gedrag. Dit betekent dat de stof noch een gas, noch een vloeistof is, maar eigenschappen heeft van beide fases. Bij superkritische condities is er dan ook geen faseovergang meer mogelijk. Een voorbeeld van een superkritische stof is superkritische kooldioxide (druk is hoger dan 73 atm. en temperatuur is hoger dan 31 °C).
De werkelijke en kritisch druk en temperatuur van een stof kunnen als volgt gebruikt worden om de gereduceerde druk en temperatuur van die stof te berekenen:
$$ p_\R = p / p_\c $$
$$ T_\R = T / T_\c $$
met:
$p_\R$, $T_\R$ = gereduceerde druk resp. temperatuur
$p_\c$, $T_\c$ = kritische druk resp. temperatuur
Vervolgens kunnen deze gereduceerde druk en temperatuur gebruikt worden om bijvoorbeeld de compressibiliteitsfactor ($Z$) te bepalen die gebruikt wordt in de toestandsvergelijking voor een reëel gas.
Tx-diagram
Wanneer een vloeistof uit een mengsel van stoffen bestaat, zal de temperatuur tijdens verdamping bij een bepaalde druk in het algemeen niet constant zijn, ook al verandert de druk niet. Doordat de stoffen verschillende kookpunten hebben, zal niet alleen de temperatuur veranderen, maar zijn ook de samenstellingen van de vloeistof- en dampfases verschillend van elkaar. In een T,x-diagram wordt bij een bepaalde druk de kooktemperatuur van het mengsel versus de samenstelling van de vloeistof- en dampfases weergegeven. De onderste curve in het diagram geeft de samenstelling van de vloeistoffase aan.
Onderstaande figuur geeft het T,x-diagram van een ideaal mengsel (ideale oplossing) weer. Ideaal wil zeggen dat de interactie tussen de moleculen van component 1 (ongeveer) hetzelfde is als tussen de moleculen van component 2 en tussen de moleculen van componenten 1 en 2. Bij een bepaalde temperatuur, bijv. bij de 'example isotherm', kan uit dit diagram de samenstelling van de dampfase (bovenste lijn) en de vloeistoffase (onderste lijn) afgelezen worden. Bij de 'example isotherm' bestaat de vloeistoffase voor ongeveer 37% uit component 1 en de dampfase voor ongeveer 15% uit component 1.
Voor het berekenen van de samenstelling van de damp- en vloeistoffases kan de wet van Raoult gebruikt worden. Ook kunnen toestandsgrootheden van tweefasesystemen berekend worden.
Toestandsgrootheden van tweefasesystemen
Bij berekeningen aan tweefasesystemen wordt ervan uitgegaan dat de gas- en vloeistoffase ideaal gemengd zijn. Voor een toestandsgrootheid M (bijv. de enthalpie H of de entropie S) van het tweefasesysteem als geheel geldt:
$$ M = xM_\g + (1-x)M_\l $$
met:
$x$ = dampfractie (in het Engels: quality)
$M_\g$ = toestandsgrootheid van de stof in de gasfase, bij de condities van het tweefasesysteem
$M_\l$ = idem, van de stof in de vloeistoffase
Bovenstaande vergelijking kan als volgt omgeschreven worden:
$$ M = xM_\g + M_\l - xM_\l = M_\l + x(M_\g - M_\l) $$
en daaruit volgt dat de dampfractie dus gelijk is aan:
$$ x = {M - M_\l} / { M_\g - M_\l } $$
Wet van Raoult
Voor de berekening van de samenstelling van de damp- en vloeistoffases kan voor (nagenoeg) ideale gassen en vloeistoffen de wet van Raoult gebruikt worden:
$$ y_i p = x_i p_i^{\sat} $$
met:
$y_i$ = molfractie van component i in de dampfase
$p$ = totale druk bij temperatuur T
$x_i$ = molfractie van component i in de vloeistoffase
$p_i ^{\sat}$ = verzadigde dampspanning van de zuivere component i bij temperatuur T
Met de wet van Raoult kunnen bijvoorbeeld de druk en samenstelling van de dampfase bij een bepaalde temperatuur berekend worden als de samenstelling van de vloeistoffase en de dampdruk van de componenten bij die temperatuur bekend zijn.
Toestandsdiagrammen
Toestandsdiagrammen zijn erg behulpzaam bij het analyseren van processen aangezien ze gebruikt kunnen worden om de hoeveelheden warmte en arbeid die uitgewisseld worden tussen systeem en omgeving te visualiseren. Voorbeelden van toestandsdiagrammen zijn p,V-, T,S- en H,S-diagrammen.
p,V-diagram
Het p,V-diagram is al eerder genoemd bij fasediagrammen. In onderstaande figuur is weergegeven hoe een ideaal gas isotherm expandeert van punt A naar punt B. Zowel aan het verloop van de lijn als aan de formule die erbij staat, is te zien dat het bij een isotherm om een omgekeerd evenredig verband tussen druk en volume gaat. De door het gas verrichte arbeid tijdens de expansie is in de figuur weergeven met het gekleurde oppervlak.
P,V-diagram van een ideaal gas dat isotherm expandeert van punt A naar punt B (bron: Wikimedia Commons)
De hoeveelheid arbeid die het gas verricht kan worden berekend met de formule: $$ W_{A→B} = {∫_{A}^{B} p \dV $$
T,S-diagram
Voor het zichtbaar maken van hoeveelheden warmte en arbeid zijn T,S-diagrammen bruikbaar. In het T,S-diagram van onderstaande figuur is een willekeurige omkeerbare (reversibele) thermodynamische cyclus afgebeeld waarbij de temperaturen liggen tussen TH en TC en de entropiewaardes tussen SA en SB. Onder de aanname dat het proces arbeid verricht (en het kringproces dus rechtsom verloopt), is het oppervlak binnen de kromme gelijk aan deze hoeveelheid arbeid en is het oppervlak QC gelijk aan de hoeveelheid warmte die overgedragen wordt van het systeem naar de omgeving. Het totaal van beide oppervlakken is de opgenomen hoeveelheid warmte QH.
H,S-diagram
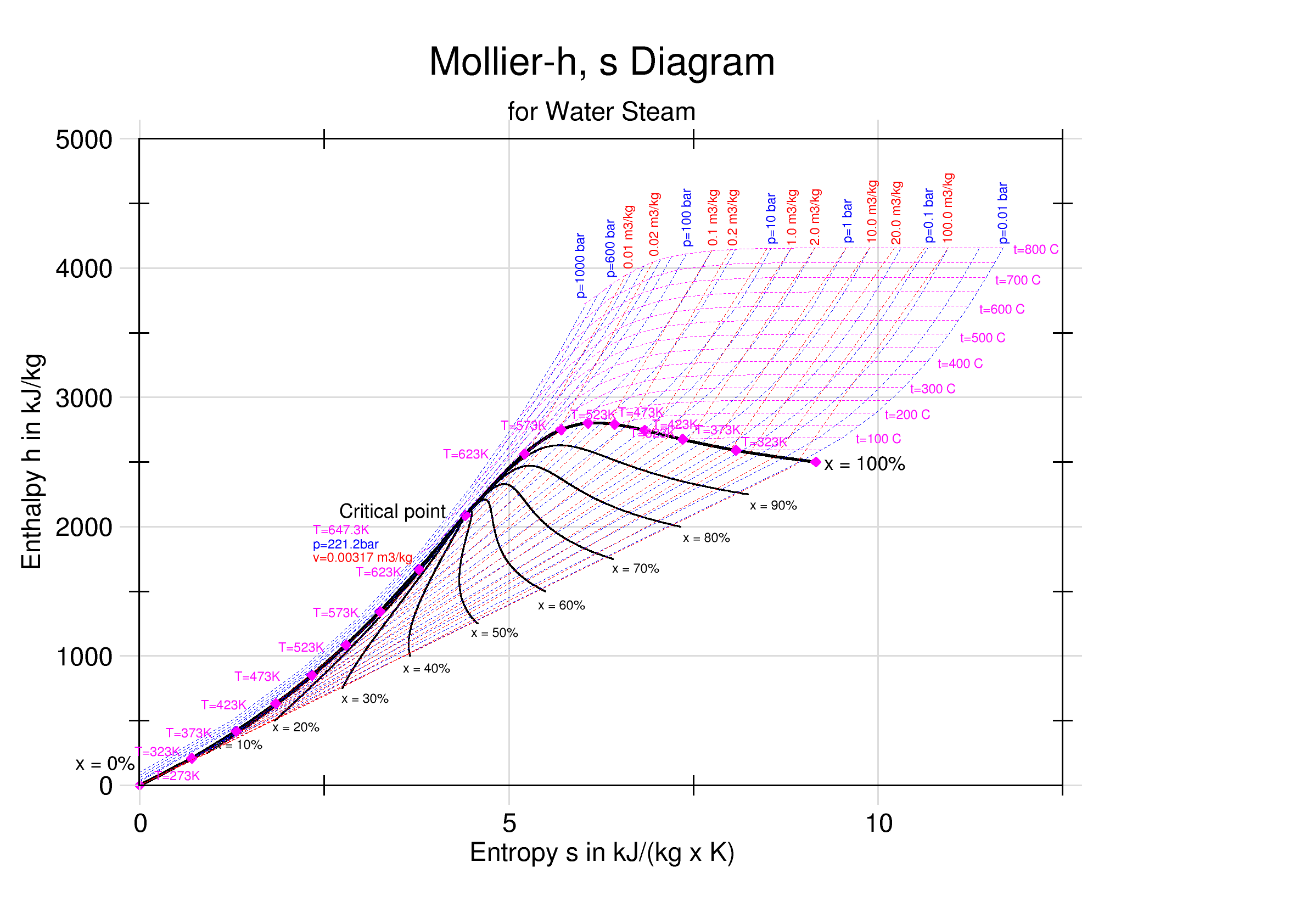
H,S-diagrammen worden vooral gebruikt voor stoom/watersystemen. Het H,S-diagram wordt ook wel een Mollier-diagram genoemd, naar de bedenker R. Mollier. Onderstaande figuur laat het Mollier-diagram voor water/stoom zien. In de figuur zijn isobaren, isothermen en lijnen met constante dampfracties (aangeduid met x) aangegeven. In het gebied omsloten door de dikke zwarte golvende curve zijn vloeistof en damp met elkaar in evenwicht en zijn de isobaren en isothermen aan elkaar gelijk.
Adiabatisch, reversibel en isentropisch
Bij kringprocessen is er vaak sprake van adiabatische processen en ook bij de berekening aan toestandsveranderingen wordt regelmatig aangenomen dat een toestandsverandering adiabatisch, reversibel en/of isentropisch verloopt. Wanneer een proces adiabatisch verloopt wil dat zeggen dat er geen warmte-uitwisseling met de omgeving is. Een proces dat niet alleen adiabatisch verloopt maar ook omkeerbaar (reversibel) wordt een isentropisch proces genoemd, m.a.w. de entropiewaarde blijft gelijk. Een isentropisch proces verloopt in een T,S- of H,S-diagram dus langs een verticale lijn.
Berekeningen aan toestandsveranderingen
Wanneer ervan uitgegaan wordt dat een gas zich ideaal gedraagt, kan de ideaal gaswet, pV = nRT, gebruikt worden voor berekeningen aan toestandsveranderingen waarbij de hoeveelheid gas hetzelfde blijft. Voor toestandsveranderingen in het algemeen, de zogenaamde polytropische toestandsveranderingen, geldt: pVn = constant. NB: n is de exponent van de polytroop, dit is niet het aantal mol gas (n) uit de ideaal gaswet! Hieronder wordt een aantal veelvoorkomende toestandsveranderingen (processen) behandeld.
Isotherme processen
Op basis van de ideaal gaswet geldt voor een isotherm proces: $$ pV = constant $$
immers, zowel n, R als T zijn constant. Zoals beschreven bij toestandsdiagrammen ziet het verloop van een isotherm proces er in een p,V-diagram uit als een omgekeerd evenredig verband tussen druk en volume.
Voor de volumearbeid uitgeoefend tijdens een isotherm proces geldt:
$$ \d W = p \d V $$
Vervangen van p door nRT/V (ideaal gaswet) en integreren levert vervolgens op:
$$ W_{\begin → \eind} = nRT \ln {V_\eind} / {V_\begin} $$
Aangezien pV constant is, geldt voor deze volumearbeid ook:
$$ W_{\begin → \eind} = nRT \ln {p_\begin} / {p_\eind} $$
De hoeveelheid warmte die gepaard gaat met dit proces kan berekend worden uit de 1e hoofdwet voor een gesloten systeem en de afhankelijkheid van de inwendige energie van de temperatuur:
$$ \Δ U = Q - W $$ resp.
$$ \Δ U = C_V \Δ T = 0 $$
Er geldt dus:
$$ Q = W $$
Isochoor proces
Bij een isochoor proces is het volume constant. In een p,V-diagram ziet een isochoor proces er dus uit als een verticale lijn. Doordat het volume niet verandert, is de volumearbeid gelijk aan nul. Uit de 1e hoofdwet voor een gesloten systeem volgt dat dan geldt:
$$ \Δ U = Q = C_V \Δ T $$
Isobaar proces
Bij een isobaar proces is de druk constant. Een isobaar proces ziet er in een p,V-diagram dus uit als een horizontale lijn. Aangezien de druk niet afhankelijk is van het volume (zoals wel het geval is bij een isotherm proces), geldt hier voor de volumearbeid:
$$ W = p(V_\eind - V_\begin) $$
Voor de hoeveelheid warmte die uitgewisseld wordt geldt (TB142E, Analyse van energiesystemen):
$$ Q = C_p \Δ T = m c_p \Δ T $$
en voor de inwendige energie geldt wederom:
$$ \Δ U = C_V \Δ T $$
Adiabatisch proces
Bij een adiabatisch proces is de uitgewisselde warmte Q gelijk aan nul. Uit de 1e hoofdwet voor een gesloten systeem volgt dan:
$$ \Δ U = C_V \Δ T = - W $$
Verder geldt voor een adiabatisch proces:
$$ pV^{(c_p/c_v)} = \constant $$
Het verloop van een adiabatisch proces in een p,V-diagram lijkt enigszins op dat van een isotherm proces, maar de lijn gaat bij een adiabaat sterker naar beneden ("maakt een diepere buiging") dan het omgekeerd evenredige verband van de isotherm.
Samenvatting
Het voorgaande kan samengevat worden in onderstaande tabel, waarbij 'n' in de laatste rij dus gelijk is aan de exponent van de polytroop pVn.
| isotherm | isochoor | isobaar | adiabaat | |
| ΔU | 0 | CVΔT | CVΔT | CVΔT |
| Q | Q = W | CVΔT | CpΔT | 0 |
| W | nRTln(Veind/Vbegin) of nRTln(pbegin/peind) | 0 | p(Veind - Vbegin) | - CVΔT |
| const. | pV | V | p | pV(cp/cv) |
| n | 1 | ∞ | 0 | cp/cv |
Achtergrondinformatie
• Youtube-filmpje over polytropische toestandsveranderingenw (deel 1 van een serie)
Introductie kringprocessen
Wat is een kringproces?
Een kringproces is een proces waarbij het medium dat het proces doorloopt na afloop van het proces weer dezelfde toestand heeft als waarmee het begon. Kringprocessen worden toegepast in warmtemotoren voor de omzetting van warmte in arbeid, warmtepompen en koelmachines. Een kringproces waarbij warmte wordt omgezet in arbeid wordt een positief kringproces genoemd. Wanneer het omgekeerde het geval is, is sprake van een negatief kringproces. Een positief kringproces draait met de klok mee in een p,V-diagram.
Reversibele en irreversibele (kring)processen
In de thermodynamica wordt onderscheid gemaakt tussen reversibele en irreversibele (kring)processen. Reversibel (omkeerbaar) wil zeggen dat een proces zonder ingreep van buitenaf op elk moment in de omgekeerde richting kan verlopen. Anders gezegd: een proces is reversibel wanneer het ook in omgekeerde richting kan verlopen op een zodanige manier dat het systeem noch de omgeving achteraf veranderd zijn. Een voorbeeld van een reversibel proces is warmteoverdracht bij oneindig kleine temperatuurverschillen. Alleen in het ideale geval verlopen processen reversibel, in werkelijkheid verlopen alle processen irreversibel.
Kringprocessen zijn veelal genoemd naar de bedenker ervan. Voorbeelden van kringprocessen zijn de Carnot-, Rankine-, Brayton-, Otto-, Stirling- en de nieuwe Allam-kringloop. Berekeningen aan kringprocessen, zoals de hoeveelheden warmte en arbeid die uitgewisseld worden tussen systeem en omgeving, kunnen uitgevoerd worden aan de hand van de condities (druk, temperatuur, volume) van het kringloopmedium tijdens de kringloop.
Achtergrondinformatie
• Allam-kringloopw (een ontwikkeling waarbij superkritische CO2 de turbine aandrijft)
Carnot-kringloop
Een van de formuleringen van de tweede hoofdwet van de thermodynamica is dat warmte niet volledig omgezet kan worden in arbeid. Tijdens het vak TB142E, Analyse van energiesystemen, is al kort behandeld dat het maximale, theoretische, rendement waarmee warmte omgezet kan worden in arbeid gegeven wordt door het Carnot-rendement, namelijk:
$$ η_\C = 1 - T_{\laag} / T_{\hoog}$$
met:
Thoog = temperatuur van de warmte die gebruikt wordt om arbeid uit te produceren [K]
Tlaag = temperatuur van de (rest)warmte die als gevolg van de 2e hoofdwet afgevoerd moet worden [K]
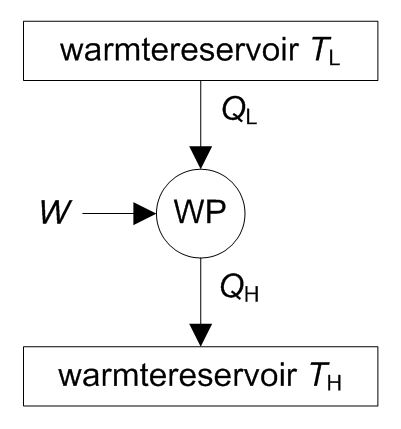
Hoe hoger de temperatuur van de warmte, hoe meer arbeid er dus uit kan worden gewonnen. Er wordt ook wel gezegd: hoe meer kwaliteit (exergie) die warmte heeft. Het Carnot-rendement is het rendement van het theoretische proces dat in 1824 door Sadi Carnot als eerste werd beschreven en waarbij warmte maximaal in arbeid wordt omgezet: het Carnot-proces. Dit Carnot-proces bestaat uit een reversibel werkende warmtemotor, de Carnot-motor, waarbij warmte door middel van een cyclisch proces wordt omgezet in arbeid. (Het omgekeerde proces is ook mogelijk, dit is dan een warmtepomp.)
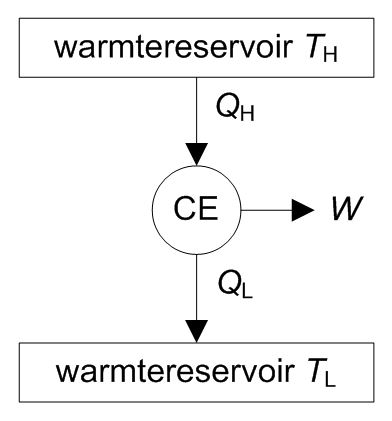
Het principe van het Carnot-proces is weergegeven in onderstaande figuur. In de figuur is te zien dat de Carnot-motor (CE, Carnot engine) warmte QH opneemt met temperatuur TH, een hoeveelheid arbeid (W) produceert en warmte QL afgeeft bij temperatuur TL.
Volgens de eerste hoofdwet geldt voor het Carnot-proces:
Het rendement van het Carnot-proces (het Carnot-rendement) is gedefinieerd als:
Volgens Carnot geldt:
Uit de voorgaande twee vergelijkingen volgt dat het Carnot-rendement gelijk is aan:
$$ η_\C = 1 - {T_\L} / {T_\H} $$
N.B.: Voor alle bovenstaande vergelijkingen geldt dat de temperatuurwaarden ingevuld dienen te worden in Kelvin.
Achtergrondinformatie
• 2e hoofdwet, Sadi Carnot en het Carnot-procesw (vanaf resp. het begin, ca. 4 minuten en ca. 5 minuten)
Rankine-kringloop
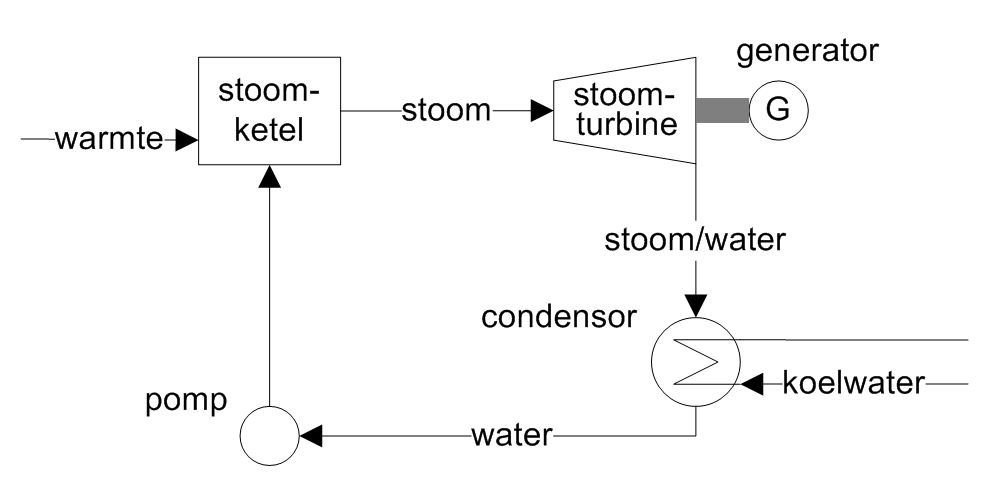
De ideale Carnot-cyclus wordt in de praktijk benaderd door de Rankine-cyclus. Hierbij is o.a. de isotherme warmtetoevoer van de Carnot-cyclus vervangen door isobare verhitting inclusief faseovergang en de isotherme warmteafvoer vindt plaats door middel van condensatie. De stoomcyclus bij elektriciteitsproductie is een uitvoeringsvorm van de Rankine-cyclus.
Een stoomcyclus (zie onderstaande figuur) bestaat in grote lijnen uit de volgende stappen (en onderdelen):
• in een stoomketel wordt verbrandingswarmte gebruikt om water via een aantal stappen om te zetten in oververhitte stoom
• deze stoom gaat naar een stoomturbine die gekoppeld is aan een generator, in de stoomturbine expandeert de stoom tot oververzadigde stoom waardoor een deel van de stoom condenseert
• het stoom/water-mengsel wordt verder gecondenseerd tot water in de condensor
• een pomp brengt het water weer op de oorspronkelijke druk
Gesteld dat de temperatuur van de stoom 415 °C is en van het koelwater 15 °C. Dan komt het Carnot-rendement, het theoretisch maximaal haalbare rendement, van de stoomcyclus uit op 58 procent. Onderstaande figuur laat het T,S-diagram van een eenvoudige, ideale Rankine-cyclus zien. De (voedingswater)pomp bevindt zich tussen de punten 1 en 2, de stoomketel tussen de punten 2 en 3, de stoomturbine tussen de punten 3 en 4 en de condensor tussen de punten 4 en 1.
Het rendement van een Rankine-cyclus is de hoeveelheid arbeid die netto geproduceerd wordt, dat wil zeggen de hoeveelheid arbeid die de turbine levert minus de benodigde arbeid benodigd voor compressie, gedeeld door de hoeveelheid warmte die toegevoerd wordt bij het verwarmen, verdampen en oververhitten van water tot stoom. In formulevorm:
$$ η = W_\net / Q_\in $$
Uitgaande van de punten in bovenstaande figuur is het rendement van deze cyclus inclusief oververhitting gelijk aan:
$$ η = {W_{\3->4} + W_{\1->2}} / Q_{\2->3} $$
en met toepassing van de eerste hoofdwet(*), wordt dit:
$$ η = {(H_3 - H_4) + (H_1 - H_2)} / {(H_3 - H_2)} $$
Bovenstaande vergelijking kan desgewenst worden omgeschreven tot:
$$ η = {|H_3 - H_4| - |H_1 - H_2|} / {|H_3 - H_2|} $$
Het rendement van een Rankine-cyclus kan verhoogd worden door de stoom te heroververhitten. Het bijbehorende T,S-diagram is te vinden in onderstaande figuur, waarbij tussen de punten a en b de heroververhitting plaatsvindt.
Uitgaande van de punten in bovenstaande figuur wordt het rendement nu:
$$ η = {(H_3 - H_a) + (H_b - H_c) + (H_1 - H_2)} / {(H_3 - H_2) + (H_b - H_a)} $$
of, anders opgeschreven:
$$ η = {|H_3 - H_a| + |H_b - H_c| - |H_1 - H_2|} / {|H_3 - H_2| + |H_b - H_a|} $$
Een andere manier om het rendement verhogen is het toepassen van een voedingswatervoorverwarmer en leidt tot onderstaand T,S-diagram. Hiervoor wordt een deel van de stoom voortijdig afgetapt bij de stoomturbine (punt a), gemengd(**) met water uit de voedingswaterpomp (punt c), verder op druk gebracht en tussen de punten (d) en (3) in een boiler verhit tot oververhitte stoom. De warmte benodigd voor het opwarmen tussen de punten (b) en (c) is afkomstig van de afgetapte stoom. Het bijbehorende schema is evt. hierw te bekijken. Combinaties van heroververhitters en voedingswatervoorverwarmers zijn uiteraard ook mogelijk.
Op basis van de punten in bovenstaande figuur geldt voor het rendement nu (turbine-arbeid wordt in twee delen berekend vanwege de aftapstroom):
$$ η = {(H_3 - H_a) + (H_a - H_4) + (H_1 - H_b) + (H_c - H_d)} / {(H_3 - H_d)} $$
of, anders opgeschreven:
$$ η = {|H_3 - H_a| + |H_a - H_4| - |H_1 - H_b| - |H_c - H_d|} / {|H_3 - H_d|} $$
(*) Voor turbines en pompen geldt dat de kinetische en potentiële energietermen evenals de uitwisseling van warmte met de omgeving verwaarloosd kunnen worden.
(**) Indien een open voedingswatervoorverwarmer wordt toegepast. Bij een gesloten voedingswatervoorverwarmer wordt warmte overgedragen dmv een warmtewisselaar en vindt menging plaats na drukverhoging tot de druk van het voedingswater.
Achtergrondinformatie
• Rankine-kringloopw (standaard- en werkelijke kringloop plus verbeteringen)
Brayton-kringloop
Bij de Brayton-cyclus is er geen sprake van isotherme toestandsveranderingen zoals bij de Carnot-cyclus, maar is zowel de warmtetoevoer als de warmteafvoer geheel isobaar. Er vindt geen faseovergang plaats en de compressie- en expansiestap verlopen beide adiabatisch en nagenoeg ook isentropisch. De Brayton-cyclus wordt toegepast bij gasturbine-installaties. Onderstaande figuur laat links een gasturbine-installatie zien en midden en rechts de ideale Brayton-cyclus in resp. een p,V- en T,S-diagram.
Het rendement van een Brayton-kringloop kan op dezelfde manier berekend worden als dat van een Rankine-kringloop, want ook hier geldt:
$$ η = W_\net / Q_\in $$
Uitgaande van de punten in bovenstaande figuur is het rendement, bij toepassing van de eerste hoofdwet(*), gelijk aan:
$$ η = {(H_3 - H_4) + (H_1 - H_2)} / {(H_3 - H_2)} $$
of, anders opgeschreven:
(*) Voor turbines en pompen geldt dat de kinetische en potentiële energietermen evenals de uitwisseling van warmte met de omgeving verwaarloosd kunnen worden.
Achtergrondinformatie
• Brayton-kringloopw (toelichting)
Stirling-kringloop
Een ideale Stirling-kringloop is een gesloten kringloop die bestaat uit twee isothermen en twee isochoren. Het kringloopmedium is een gas of lucht en blijft tijdens de hele kringloop gasvormig. De ideale kringloop bestaat uit de volgende vier stappen:
• tijdens warmtetoevoer van buitenaf vindt isotherme expansie plaats (druk neemt hierbij af),
• bij constant volume wordt warmte afgevoerd naar een regenerator (druk en temperatuur nemen af),
• tijdens isotherme compressie wordt warmte naar buiten afgevoerd (volume neemt af naar beginvolume, druk neemt iets toe)
• bij constant volume wordt warmte uit de regenerator weer toegevoerd (druk en temperatuur nemen toe naar begindruk en -temperatuur)
Het maximale rendement van een Stirling-kringloop is gelijk aan het Carnot-rendement. De omgekeerde Stirling-kringloop wordt gebruikt voor cryogene koeling.
Achtergrondinformatie
• Stirling-kringloopw (toelichting, zie ook de faq over toepassingen)
Soorten elektriciteitscentrales
In Nederland worden verschillende typen elektriciteitscentrales gebruikt met een gemiddeld landelijk rendement voor de elektriciteitsproductie van circa 42%. Tijdens het vak TB142E, Analyse van energiesystemen, is al kort ingegaan op de verschillende soorten elektriciteitscentrales (thermische centralesw). In dit vak wordt uitgebreider ingegaan op de verschillen die er zijn en wordt ook ingegaan op brandstofcellen en zon-pV.
Veelvoorkomende typen (thermische) elektriciteitscentrales zijn:
• gasturbine-eenheid: een centrale gebaseerd op een gasturbine gebruikt (aard)gas als brandstof en heeft een elektrisch rendement van 20-35%.
• conventionele eenheid: de conventionele eenheid maakt gebruik van een stoomturbine. Als brandstof kan gas (aardgas/hoogovengas/...), steenkool/poederkool of bijvoorbeeld biomassa gebruikt worden, maar de benodigde stoom kan ook geproduceerd worden met warmte afkomstig van bijvoorbeeld kernreacties, zonne-energie en thermische energieopslag. Het rendement is 35-40%.
• gasgestookte combi-eenheid: hierbij is sprake van zowel een gas- als een stoomturbine. De stoomturbine is het grootst. In de gasturbine wordt (aard)gas verbrand, deze drijft een eigen generator aan. De hete uitlaatgassen van de gasturbine worden gebruikt als verbrandingslucht voor de verbranding van (aard)gas in de stoomketel. Het rendement is 40-45%.
• STEG (SToom En Gasturbine)-eenheid: bij een STEG-eenheid is de gasturbine het grootst. Mogelijke brandstoffen zijn (aard)gas en gereinigd synthesegas afkomstig van de vergassing van bijvoorbeeld biomassa, steenkool of een andere koolstofhoudende (afval)stroom. De verbrandingsgassen die de gasturbine verlaten worden gebruikt voor stoomproductie in de stoomcyclus. Er wordt dus geen aparte brandstof gebruikt voor de stoomcyclus. De stoom- en gasturbine drijven samen dezelfde generator aan. Het rendement is 50-60%. In onderstaande figuur zijn beide thermodynamische kringlopen van een STEG te zien. Tussen de punten 4 en 1 draagt het kringloopmedium van de Brayton-kringloop warmte over naar het kringloopmedium van de Rankine-kringloop, dat de warmte tussen de punten a en d opneemt.
Een belangrijk kenmerk van elektriciteitscentrales is het behaalde rendement voor elektriciteitsproductie. Bij de interpretatie van rendementen is het van groot belang te weten hoe het rendement precies gedefinieerd is.
Basis-, midden- en pieklast
De elektriciteitsbehoefte varieert per etmaal. Zo is er ‘s nachts minder elektriciteit nodig dan overdag. De lage elektriciteitsbehoefte ‘s nachts wordt basislast genoemd. Daarnaast worden midden- en pieklast onderscheiden. Op werkdagen is overdag sprake van middenlast. Van pieklast is sprake wanneer er overdag op werkdagen extra behoefte is aan elektriciteit. Aangezien elektriciteit moeilijk grootschalig opgeslagen kan worden, wordt de productie afgestemd op de vraag. Bij de vervulling van de verschillende elektriciteitsbehoeften (basis-, midden- en pieklast) wordt rekening gehouden met de eigenschappen (regelbaarheid) en kosten van de diverse elektriciteitscentrales. Voor basislastvermogen worden elektriciteitscentrales ingezet die langdurig op vol vermogen kunnen draaien, zoals kolencentrales. Deze centrales hebben relatief hoge vaste kosten en lage variabele kosten. Voor middenlastvermogen worden STEG- en combi-eenheden ingezet. Voor het pieklastvermogen worden eenheden ingezet die snel op te starten zijn, zoals gasturbines. Deze eenheden hebben relatief lage vaste kosten en hoge variabele kosten.
Warmtekrachtkoppeling
Bij warmtekrachtkoppeling (WKK) is sprake van elektriciteitsproductie gecombineerd met de productie van bruikbare warmte. Er bestaan vele verschillende uitvoeringsvormen van warmtekrachtkoppeling. Een veelgebruikte installatie voor de productie van elektriciteit en warmte is een STEG-eenheid. De Engelse benaming voor WKK is CHP (Combined Heat and Power).
De afkorting WKC staat voor WarmteKrachtCentrale. Volgens de Carnot-kringloop komt er bij de productie van elektriciteit uit warmte altijd een hoeveelheid restwarmte vrij. Bij een warmte-kracht¬centrale wordt deze restwarmte niet weggekoeld maar nuttig gebruikt, bijvoorbeeld als proceswarmte in de industrie. Deze nuttig te gebruiken (proces)warmte heeft een hogere temperatuur dan de weg te koelen restwarmte zou hebben. De hogere temperatuur van de geproduceerde warmte gaat ten koste van het elektrische rendement van de elektriciteits-productie. Het elektrische rendement van een WKC is lager dan van een elektriciteits¬centrale die alleen elektriciteit produceert.
Het voordeel van een WKC is dat de brandstof zo efficiënt mogelijk gebruikt wordt voor de productie van elektriciteit en warmte. Het ligt daarom voor de hand een WKC te bouwen op een plaats waar de warmte altijd nuttig gebruikt kan worden, bijvoorbeeld in de nabijheid van warmtevragende procesindustrie. Wanneer de warmte van een WKC weggekoeld zou moeten worden en men dus alleen de geproduceerde elektriciteit nuttig gebruikt, had een gewone elektriciteitscentrale efficiënter geweest.
Achtergrondinformatie
• Youtube-filmpje kolencentralew (conventionele kolencentrale incl rookgasreiniging)
• Youtube-filmpje STEGw (uitleg principe)
Definities van rendementen
De definitie van een rendement hangt samen met de keuze van de systeemgrenzen. Bij het rendement van een elektriciteitscentrale is het bijvoorbeeld van belang te weten of het interne elektriciteitsverbruik van de centrale wel of niet in mindering is gebracht op de geproduceerde hoeveelheid elektriciteit. En wordt bij een huishoudelijke HR-ketel gerekend met de verbrandingswaarde of de stookwaarde van het aardgas? In het laatste geval kan het rendement hoger uitkomen dan 100% ...
Rendementen zijn afhankelijk van de absolute waarden van de stromen. Stel je hebt een proces waarbij de hoeveelheid energie in de productstroom 1 MW minder is dan de toegevoerde hoeveelheid energie aan het proces. Wanneer de toegevoerde hoeveelheid energie 100 MW is, komt het energierendement uit op (100-1)/100 = 99%. Maar wanneer de toegevoerde hoeveelheid energie slechts 5 MW is, bedraagt het energierendement (5‑1)/5 = 80%. Een aanzienlijk verschil in energierendement, terwijl het energiegebruik (het verschil tussen toegevoerde hoeveelheid energie en energie in de productstroom) onveranderd 1 MW is. Een alternatief voor het werken met rendementen is bijvoorbeeld energiegebruik per hoeveelheid product.
Er zijn verschillende manieren om rendementen te definiëren, bijvoorbeeld universele en functionele rendementen. Bij het vergelijken van prestaties van processen is het verder van belang dat de te vergelijken processen ook daadwerkelijk vergelijkbaar zijn. Stel dat er twee processen vergeleken worden waarbij in proces A verbranding plaatsvindt met lucht, terwijl daarvoor in proces B zuivere zuurstof gebruikt wordt. Voor een goede technologische vergelijking zou dan bij de bepaling van de prestatie van proces B een zuurstoffabriek meegenomen moeten worden in de berekening.
Uitgaande van een temperatuur van ca. 1100 °C van de verbrandingsgassen en ca. 15 °C voor het koelwater, is het Carnot-rendement van elektriciteitsproductie 79%. Het werkelijke rendement is vanzelfsprekend lager en is afhankelijk van het type elektriciteitscentrale.
Regelbaarheid van elektriciteitscentrales
Wanneer er op een bepaald moment meer elektriciteit geproduceerd wordt dan er vraag is, kan worden overgegaan tot het bedrijven in deellast. Dit houdt in dat een installatie niet op vol vermogen draait maar dat er minder brandstof wordt verwerkt dan waarvoor de installatie ontworpen is. Het bedrijven in deellast is veelal nadelig voor het rendement van de installatie. Ook kan er dan vervuiling optreden doordat stofdeeltjes bij lagere gassnelheden de kans krijgen om zich in de installatie af te zetten en kunnen er instabiliteiten in het stoomsysteem ontstaan waardoor de kwaliteit van de stoom niet meer aan de eisen voldoet (Dijkema et al. (2009)w). De minimumcapaciteit waarop elektriciteitscentrales kunnen werken is ongeveer 30 procent van de ontwerpcapaciteit. De snelheid waarmee de capaciteit van grote, conventionele gas- en kolencentrales geregeld kan worden is ongeveer 2 procent per minuut (Dijkema et al. (2009). Wanneer de elektriciteitsvraag hoger is, kunnen de meeste elektriciteitscentrales tijdelijk ook meer elektriciteit leveren, tot ongeveer 105 procent van de ontwerpcapaciteit. Dit kan niet gedurende lange tijd want dan zou er excessieve schade en/of slijtage ontstaan (Dijkema et al. (2009)). Bij het regelen van het vermogen hebben de operators te maken met de responstijd (de tijd tussen het uitvoeren van een regelactie en het moment dat er een verandering waarneembaar is) en de traagheid (hoe lang het duurt van het begin van de verandering tot aan het moment dat de centrale op het nieuwe vermogen werkt).
Elektriciteitscentrales kunnen niet ineens aan- en uitgezet worden. Dit moet geleidelijk gebeuren om schade aan de installatie te voorkomen. Wanneer de temperatuur te snel toe- of af zou nemen zorgt dit voor spanningen in de wanden van de apparatuur wat de levensduur van deze apparatuur niet ten goede komt. Er kan bijvoorbeeld kruip (blijvende vervorming van een materiaal) en vermoeiing (afname materiaalsterkte, kans op breuk) optreden. Hoe hoger de druk in de apparatuur, hoe dikker de wanden en hoe groter de kans op spanningen in deze wanden bij temperatuurverandering. Dit betekent dat gasturbines sneller opgestart kunnen worden dan stoomturbines en dat kleinere stoomturbines, die bij lagere drukken werken, sneller opgestart kunnen worden dan grote stoomturbines. Een gasturbine die niet bij al te hoge drukken werkt, kan in ongeveer 20 minuten op vol vermogen draaien. Bij een stoomturbine die op hoge drukken werkt (275 – 150 bar) kost dit 3 tot 6 uur. Onderstaande tabel geeft een overzicht van capaciteit, opstarttijd, minimaal aantal uren dat de centrale vervolgens in bedrijf moet zijn en de regelsnelheid van een aantal typen elektriciteitscentrales (Dijkema et al. (2009)).
| Type | Capaciteit [MW] | Opstarttijd [uren] | Min Up [uren] | Regelsnelheid [MW/min] |
| Poederkool | 500-700 | 6 | 24 | 15-20 |
| Gasturbine-eenheid | 10-25 | << 1 | 1 | 1-2 |
| STEG | 120-350 | 2 | 4 | 4-10 |
| Combi-eenheid | 350 | 5,5 | 4 | 10-20 |
| Gasmotor | < 1 | n.v.t. | n.v.t. | |
| Kerncentrale | 450 | NA | NA | 14 |
Onderdelen van elektriciteitscentrales
Belangrijke onderdelen van elektriciteitscentrales zijn de verbrandingsoven, de overdracht van warmte van rookgassen naar de water/stoomcyclus, pompen, compressoren en ventilatoren, turbines en generatoren.
Verbrandingsoven
In een verbrandingsoven of ketel wordt een brandstof verbrand en worden de ontstane hete rookgassen gebruikt om heet water of stoom te produceren. Het rendement van een verbrandingsoven is gedefinieerd als de warmte die wordt opgenomen door het water gedeeld door de hoeveelheid verbrandingswarmte die vrijkomt. Dit wordt het waterzijdig rendement genoemd. In formulevorm:
$$ η_{\stoomproductie} = {H_{\uit,\water\/\stoom} - H_{\in,\water\/\stoom}} / {Q_\verbranding} $$
Om zeker te zijn van volledige verbranding van de brandstof wordt ervoor gezorgd dat er meer zuurstof aanwezig is dan nodig voor stoechiometrische verbranding. Er zijn verschillende indicatoren om deze overmaat in uit te drukken, een daarvan is de air factor. De air factor is gedefinieerd als de werkelijke oxidant-brandstofverhouding gedeeld door de stoechiometrische oxidant-brandstofverhouding (TU Delft (n.d.)). Volgens Woudstra (2012) wordt bij gasvormige brandstoffen gewoonlijk een air factor van lager dan 1,1 aangehouden en bij vaste brandstoffen gewoonlijk een air factor die hoger is dan 1,1. De air factor is van invloed op het netto elektriciteitsrendement, zie hiervoor de werkcolleges.
Verbrandingsovens zijn er in verschillende uitvoeringsvormen, zoals de verbranding op roosters en in wervelbedden. De warmteoverdracht van rookgassen naar water/stoom wordt hierna beschreven.
Warmteoverdracht
Bij elektriciteitscentrales vindt op een aantal plaatsen warmteoverdracht plaats. Een daarvan is de overdracht van de warmte van de hete rookgassen naar een stoomcyclus. Op verschillende plaatsen in de verbrandingsoven bevinden zich buizen met water en/of stoom dat opgewarmd wordt door de hete gassen daaromheen. De buizen zijn zo in de verbrandingsoven geplaatst dat de hete rookgassen achtereenvolgens worden gebruikt om water te verdampen tot stoom, geproduceerde stoom te oververhitten en het water voor te verwarmen. Een andere manier om warmte op water/stoom over te dragen is niet het water maar de rookgassen door buizen te laten stromen, waarbij de buizen zich in een ketel met het te verwarmen water bevinden. Dit wordt bijvoorbeeld toegepast in de afgasketel die gebruikt wordt bij gasturbines.
Aangezien de stoomcyclus in een elektriciteitscentrale een kringproces is, is er een condensor nodig om ervoor te zorgen dat er weer alleen vloeibaar water wordt teruggevoerd naar de verbrandingsoven. De condensatiewarmte kan afgevoerd worden met koelwater uit bijvoorbeeld een rivier of de zee of met koelwater dat door een koeltoren geleid wordt.
Er bestaan verschillende uitvoeringsvormen van warmtewisselaars voor het uitwisselen van warmte tussen twee vloeistofstromen, zie bijvoorbeeld het webdictaat van TB241Ew en Perry and Green (2008). Een daarvan is de zogenaamde ‘double-tube’-warmtewisselaar, waarbij de ene vloeistof door een buis stroomt die omgeven wordt door een wijdere buis waardoor de andere vloeistof stroomt.
Voor het rendement van warmteoverdracht wordt verwezen naar de informatie over universele en functionele exergierendementen.
Stoom- en gasturbines
In een stoomturbine wordt de energie die de stoom heeft ten gevolge van zijn hoge druk en temperatuur omgezet in bewegingsenergie van de as van de turbine. Een stoomturbine bestaat uit straalbuizen en loop- en leischoepen. In de straalbuizen expandeert de stoom waardoor de stoom een hoge snelheid krijgt. Deze stoom wordt vervolgens tussen loopschoepen door geleid waardoor het loopwiel en daarmee ook de as van de turbine gaat draaien. Aan de as zijn verschillende rijen met loopschoepen gemonteerd. Tussen deze rijen met loopschoepen bevindt zich telkens een rij leischoepen waarin de stoom verder expandeert en waarmee richting wordt gegeven aan de stoom (richting de volgende rij loopschoepen).
Voor een turbine geldt dat de kinetische en potentiële energietermen evenals de uitwisseling van warmte met de omgeving verwaarloosd kunnen worden. De eerste hoofdwet vereenvoudigt hiermee tot:
$$ \ΔH = - W $$
Oftewel:
$$ W = H_{\in} - H_{\uit} $$
In werkelijkheid zal de enthalpie van de stroom die de turbine verlaat hoger zijn dan de enthalpiewaarde die in het ideale (= isentropische) geval gehaald zou worden. Het rendement van een stoomturbine is gedefinieerd als:
$$ η_{\turbine} = W_{\actual}/ W_{\isentropic} $$
ofwel:
$$ η_{\turbine} = (H_{\in} - H_{\uit,\actual})/(H_{\in} - H_{\uit,\isentropic}) $$
Voor het bepalen van het rendement van een stoomturbine en/of de condities van een van de stromen kan het Mollier-diagram gebruikt worden. Het geheel van stoomturbine, condensor, voedingwaterpomp en verbrandingsoven/warmtetoevoer wordt een stoomturbine-installatie genoemd. De cyclus die een stoomturbine-installatie doorloopt is de Rankine-cyclus.
De werking van een gasturbine is analoog aan die van een stoomturbine met het verschil dat in een gasturbine verbrandingsgassen met een hoge druk en temperatuur expanderen. De gasturbine vormt samen met een compressor en een verbrandingskamer de gasturbine-installatie, zie de linker afbeelding in onderstaande figuur. De compressor zit op dezelfde as als de gasturbine en zorgt voor compressie van de verbrandingslucht. De verbranding vindt plaats bij deze hogere druk. De thermodynamische cyclus die doorlopen wordt in een gasturbine-installatie is de open Brayton-cyclus met lucht als medium.
Evenals voor een stoomturbine geldt bij een gasturbine:
$$ W = H_{\in} - H_{\uit} $$
Voor het rendement van een ideaal opererende gasturbine-installatie, waarbij onder andere is aangenomen dat de lucht en de verbrandingsgassen dezelfde stofconstantes hebben, geldt:
$$ η = W / Q = {(T_{\verbr} - T_{\uit}) - (T_{\compr} - T_{\in})} / {T_{\verbr} - T_{\compr}} $$
met:
Tverbr = temperatuur van de rookgassen na de verbranding
Tcompr = temperatuur van de lucht na compressie
Pompen, compressoren en ventilatoren
Een pomp wordt gebruikt om een vloeistof te verplaatsen (snelheid te geven) of in druk te verhogen. Bij gassen wordt onderscheid gemaakt tussen compressoren, die gebruikt worden om de druk van een gas te verhogen, en ventilatoren, die gebruikt worden om een gas te laten stromen. Een ventilator wordt bijvoorbeeld gebruikt in een elektriciteitscentrale om de lucht voor de verbranding aan te zuigen.
Bij pompen, compressoren en ventilatoren kan een onderverdeling gemaakt worden in apparaten die centrifugaalkrachten gebruiken, apparaten die gebruik maken van verdringing en overige apparaten. Apparaten die centrifugaalkrachten gebruiken behoren tot de turbomachines: een schoepensysteem maakt een roterende beweging en wisselt energie uit met een gas- of vloeistofstroom. Een veelgebruikte (turbo)pomp in de industrie is de centrifugaalpomp, zie onderstaande figuur. Ook de circulatiepomp van de huishoudelijke CV-installatie behoort tot de centrifugaalpompen.

Centrifugaalpomp, waarbij nummers 1a, 3 en 5 de behuizing aangeven, 2 de waaier, 4 de asafdichting en 6 de draaias. (bron: Wikimedia Commons)
Bij de apparaten die gebruik maken van verdringing, ook wel volumetrische machines genoemd, wordt er per omwenteling een bepaald volume vloeistof of gas verplaatst. Een voorbeeld van een verdringingspomp is de zuigerpomp. Onderstaande figuur laat een voorbeeld zien van een zuigerpomp met twee uitwendige kleppen.
Bij de definitie van het rendement van een pomp of compressor wordt dezelfde gedachtengang gebruikt als bij de definitie van het rendement van een stoomturbine. Namelijk, in werkelijkheid is er meer arbeid nodig dan in het ideale geval en dus geldt er:
$$ η_{\pomp\/\compressor} = W_{\isentropic} / W_{\actual} $$
ofwel:
$$ η_{\pomp\/\compressor}= (H_{\in} - H_{\uit,\isentropic}) / (H_{\in} - H_{\uit,\actual}) $$
Generatoren
Aan de as van een gas- of stoomturbine bevindt zich generator die ervoor zorgt dat de bewegingsenergie van de as wordt omgezet in elektrische energie. Generatoren maken gebruik van het feit dat er een stroom gaat lopen wanneer een geleider (spoel) zich in een veranderend magnetisch veld bevindt. Generatoren bestaan dus uit een geleider en magneten. De rendementen van generatoren gebruikt in elektriciteitscentrales zijn hoog, zo’n 98 à 99 procent.
De gegenereerde elektriciteit wordt vervolgens getransporteerd naar de afnemers en in beperkte mate ook wel opgeslagenw voor later gebruik.
Achtergrondinformatie
• elektriciteitscentralesw (veel informatie over elektriciteitscentrales en onderdelen daarvan)
Warmtepompen
Warmtepompen zorgen ervoor dat warmte van lage temperatuur, bijvoorbeeld uit de omgeving, op een hogere temperatuur wordt gebracht. Warmtepompen kunnen ook dienst doen als koelmachine. In het laatste geval is het handhaven van de lage temperatuur het doel, denk hierbij aan een koelkast waarbij de verwarmde lucht aan de achterkant van de koelkast wordt afgevoerd. Voor de optimale plaatsing van een warmtepomp in een (industriële) installatie kan gebruik worden gemaakt van Pinch-analyse.
Er bestaan verschillende soorten warmtepompen. Voorbeelden zijn compressiewarmtepompen, absorptiewarmtepompen en combinaties daarvan.
Compressiewarmtepompen
De compressor van compressiewarmtepompen kan aangedreven worden door een gasgestookte of een elektrische motor. Het medium dat de kringloop doorloopt wordt arbeidsmedium genoemd en in het geval van een koelmachine ook wel koudemiddel. Een voorbeeld van een koudemiddel is ammoniak (NH3).
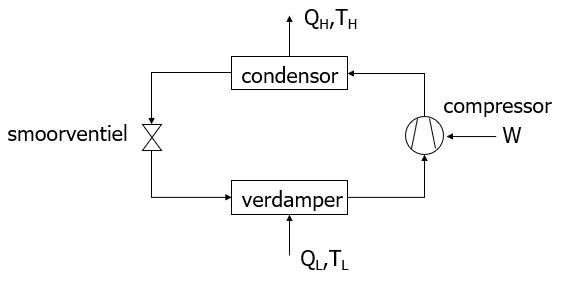
Het principe van een compressiewarmtepomp is weergegeven in onderstaande figuur.
In werkelijkheid bestaat een compressiewarmtepomp uit een verdamper (waar de warmte van lage temperatuur wordt opgenomen), een compressor (waarmee de druk verhoogd wordt en waardoor de temperatuur van het kringloopmedium stijgt van laag naar hoog), een condensor (waar de warmte van hoge temperatuur wordt afgegeven) en een smoorventiel (waarmee de druk weer verlaagd wordt tot de begindruk), zie onderstaande figuur.
Het rendement van een compressiewarmtepomp, niet zijnde een koelmachine, is gedefinieerd als de geproduceerde hoeveelheid warmte van hoge temperatuur gedeeld door de benodigde arbeid om de warmtepomp te bedrijven. Dit rendement (γ) wordt de ‘coefficient of performance’ (COP) van een warmtepomp genoemd, in formulevorm:
$$ γ_{\compr.\wp} = {\COP} ≡ {Q_\H} / {W} $$
De COP van een warmtepomp is altijd groter dan 1, d.w.z. groter dan 100%. Dit komt doordat de toegevoerde warmte van lage temperatuur niet wordt meegerekend bij de bepaling van het rendement. Uit de eerste hoofdwet en de Carnot-vergelijkingen is af te leiden dat voor het maximale (= theoretische) rendement van een compressiewarmtepomp onderstaande formule geldt:
$$ γ_{\compr.\wp,\max} = {T_\H} / {T_\H - T_\L} $$
Uit omschrijven van de formule volgt dat het maximale rendement van een compressiewarmtepomp, niet zijnde een koelmachine, dus gelijk is aan het omgekeerde Carnot-rendement:
$$ γ_{\compr.\wp,\max} = {1} / {1 - {T_\L} / {T_\H}} $$
In de praktijk bedraagt het rendement 50-70% van het theoretische (= maximale) rendement. Het verschil tussen werkelijk en theoretisch rendement wordt met name veroorzaakt doordat de expansie in het smoorventiel niet-omkeerbaar verloopt. Ook de compressiestap is niet-omkeerbaar en daarnaast zijn er temperatuurverschillen nodig in verdamper en condensor.
Bij een warmtepomp die dienst doet als koelmachine wordt het rendement (β) gedefinieerd als de hoeveelheid warmte onttrokken aan de te koelen ruimte gedeeld door de daarvoor benodigde arbeid:
$$ β_{\compr.\wp} ≡ {Q_\L} / {W} $$
Het maximale rendement van een koelmachine is:
$$ β_{\compr.\wp,\max} = {T_\L} / {T_\H - T_\L} $$
Absorptiewarmtepompen
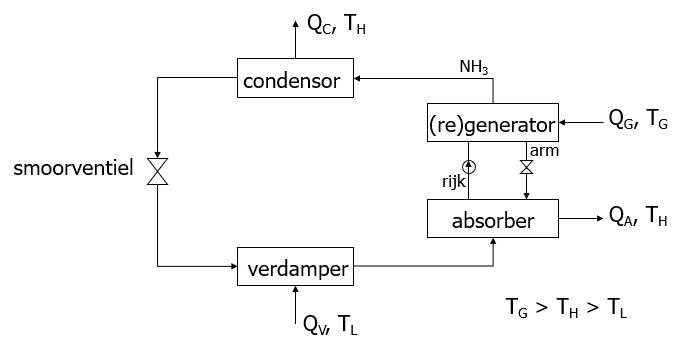
Bij absorptiewarmtepompen is geen compressor aanwezig, maar wordt de warmtepomp aangedreven door thermische energie (warmte). De compressor is in dit geval vervangen door een tweede kringloop, ook wel oplossingskringloop genoemd, waarin zich een (re)generator en een absorber bevinden, zie onderstaande figuur.
Het kringloopmedium dat door de verdamper en condensor, de koudekringloop, stroomt is bijvoorbeeld ammoniak. In de absorber lost het ammoniakgas dat uit de verdamper komt op in water. Bij dit oplossen komt warmte (QA) vrij met dezelfde temperatuur als de warmte die vrijkomt uit de condensor (QC). Het ammoniak/water mengsel wordt door middel van een vloeistofpomp in druk verhoogd en naar de (re)generator gevoerd. In de (re)generator wordt warmte (QG) toegevoerd waardoor het ammoniak uit het mengsel verdampt. De ammoniakdamp gaat naar de condensor en het water wordt na het verlagen van de druk via een smoorventiel weer teruggevoerd naar de absorber. De totale hoeveelheid geleverde warmte bestaat dus uit de warmte die vrijkomt bij absorber en condensor. Evenals compressiewarmtepompen kunnen absorptiewarmtepompen gebruikt worden om te verwarmen en te koelen.
Met verwaarlozing van de pomparbeid nodig voor de oplossingskringloop geldt, analoog aan de algemene definitie van een universeel rendement, voor het rendement van een absorptiewarmtepomp die gebruikt wordt om te verwarmen:
$$ γ_{\abs.\wp} ≡ {Q_\A + Q_\C} / {Q_\G} $$
en om te koelen:
$$ β_{\abs.\wp} ≡ {Q_\V} / {Q_\G} $$
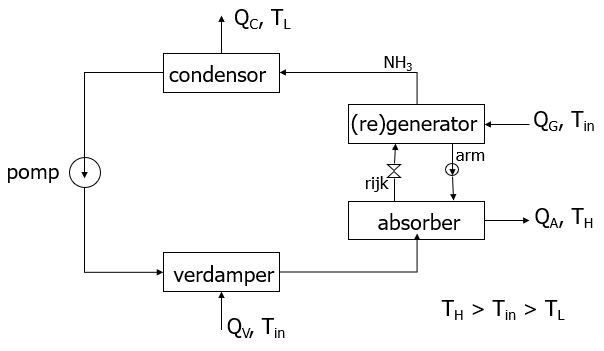
Bij een absorptiewarmtepomp die gebruikt wordt als warmtetransformator, zie onderstaande figuur, is de temperatuur van de warmte die vrijkomt bij de absorber (QA met temperatuur TH) hoger dan de temperatuur van de toegevoerde warmte bij generator en verdamper (QG resp. QV bij Tin). In dit geval opereren de verdamper en de absorber bij een hogere druk dan de generator en de condensor: tussen condensor en verdamper zit een pomp die de druk verhoogt (in plaats van een smoorventiel dat de druk verlaagt), het rijke mengsel dat van absorber naar generator gaat wordt met een smoorventiel in druk verlaagd (in plaats van in druk verhoogd met een pomp) en het arme mengsel dat teruggaat van generator naar absorber wordt met een pomp in druk verhoogd. Voor de warmtetoevoer bij de verdamper en de generator wordt warmte van dezelfde temperatuur (Tin) gebruikt. Bij een warmtetransformator is de temperatuur van de warmte die afgevoerd wordt bij de condensor (TL) het laagst: TH > Tin > TL.
Met verwaarlozing van de pomparbeid geldt, analoog aan de algemene definitie van een universeel rendement, voor het rendement van de hiervoor beschreven warmtetransformator:
$$ γ_{\warmtetransformator} ≡ {Q_\A} / { Q_\V + Q_\G} $$
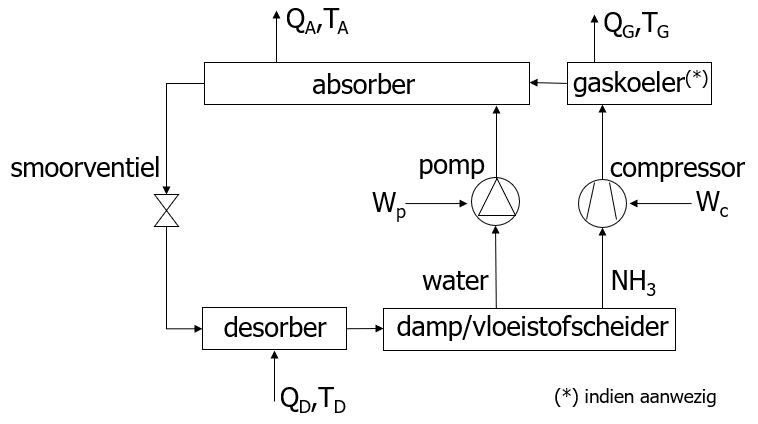
Hybride absorptie-compressiewarmtepompen
In tegenstelling tot conventionele compressie- en absorptiewarmtepompen is er bij een hybride absorptie-compressiewarmtepomp, zie onderstaande figuur, sprake van een veranderende temperatuur tijdens de absorptie/condensatie van ammoniak in water en de desorptie/verdamping van ammoniak uit water. Het voordeel van dit type warmtepompen is dat ze een hoger rendement hebben en dat de temperatuur van de productwarmte hoger is. Tijdens de desorptie/verdamping wordt lage-temperatuurwarmte (QD) gebruikt om ammoniak uit het ammoniak/water-mengsel te verdampen. Hierbij stijgt de temperatuur en ontstaat er een ammoniakrijke damp en een waterstroom met weinig ammoniak. Na scheiding van de damp- en vloeistoffasen wordt de damp gecomprimeerd en de vloeistof met een pomp in druk verhoogd. Afhankelijk van het systeemontwerp stijgt de temperatuur van de damp tijdens compressie zodanig dat een gaskoeler wordt gebruikt om de damp te koelen voordat deze naar de absorber gaat. De afgevoerde warmte bij de gaskoeler (QG) behoort dan ook tot de productwarmte. De vloeistoffase moet juist, door interne warmtewisseling met de vloeistofstroom uit de absorber, bijgewarmd worden om de juiste temperatuur te bereiken. Wanneer de damp- en vloeistofstromen samenkomen in de absorber wordt ammoniak uit de dampfase geabsorbeerd in de vloeistoffase. Hierbij komt absorptiewarmte (QA) vrij en daalt de temperatuur van de vloeistoffase doordat de verzadigingstemperatuur van ammoniak lager is dan die van water. Na de absorber (en de interne warmtewisseling met de vloeistofstroom afkomstig van de pomp) wordt de druk van de ammoniakrijke vloeistof verlaagd in het smoorventiel waardoor een damp/vloeistofmengsel bij lage temperatuur ontstaat dat weer naar de desorber/verdamper gaat.
Analoog aan de algemene definitie van een universeel rendement zijn de rendementen van de hiervoor beschreven hybride absorptie-compressiewarmtepompen met als doel verwarmen resp. koelen gelijk aan:
$$ γ_{\abs –\compr.\wp} ≡ {Q_\A (+ Q_\G)} / {W_\compressor + W_\pomp} $$
$$ β_{\abs –\compr.\wp} ≡ {Q_\D} / {W_\compressor + W_\pomp} $$
Achtergrondinformatie
• warmtepompenw (werkingsprincipe)
• warmtepompenw (idem, ook verschillende soorten)
Pinch-analyse
Pinch-analyse is veelgebruikte methode voor het optimaliseren van warmtewisselaarnetwerken. De methode is in de jaren '70 bedacht door Bodo Linnhoffw en wordt wereldwijd toegepast. Het toepassen van Pinch-analyse zorgt ervoor dat er zo goed mogelijk warmte wordt uitgewisseld tussen stromen en dat er daardoor niet meer warmte van buitenaf wordt toegevoerd en weggekoeld dan nodig. Dit leidt tot vermindering van energiegebruik en kosten.
De methode begint met het in kaart brengen van de op te warmen (= koude) en af te koelen (= warme) processtromen inclusief begin- en eindtemperatuur en hun warmtecapaciteit. Vervolgens worden de gegevens over de koude stromen gecombineerd tot een zogenaamde 'cold composite curve', waarbij de totale enthalpieverandering per temperatuurtraject wordt bepaald. De gegevens over de warme processtromen worden gebruikt voor het bepalen van de 'hot composite curve'.
Bijvoorbeeld, stroom A moet opgewarmd worden van 30 naar 80 °C en stroom B van 50 naar 100 °C:
• bij het temperatuurtraject van 30 naar 50 °C gaat het alleen om stroom A: de totale enthalpieverandering in dit traject is gelijk aan Cp,A·(50-30).
• bij het opwarmen van 50 naar 80 °C gaat het om beide stromen: de totale enthalpieverandering gelijk aan (Cp,A + Cp,B)·(80-50).
• bij het laatste deel van het temperatuurtraject gaat het alleen om stroom B: de totale enthalpieverandering gelijk aan Cp,B·(100-80).
• de ligging van de composite curve wordt bepaald door de enthalpiewaarde bij de laagste temperatuur van de stromen, in dit geval 30 °C, gelijk aan nul te stellen en daar per temperatuurinterval de betreffende totale enthalpieverandering bij op te tellen, ofwel bij 50 °C hoort een enthalpiewaarde van Cp,A·(50-30), bij 80 °C is het Cp,A·(50-30) + (Cp,A + Cp,B)·(80-50) en bij het eindpunt van deze composite curve, namelijk 100 °C, is de enthalpiewaarde gelijk aan Cp,A·(50-30) + (Cp,A + Cp,B)·(80-50) + Cp,B·(100-80).
Hetzelfde principe wordt toegepast bij de af te koelen stromen.
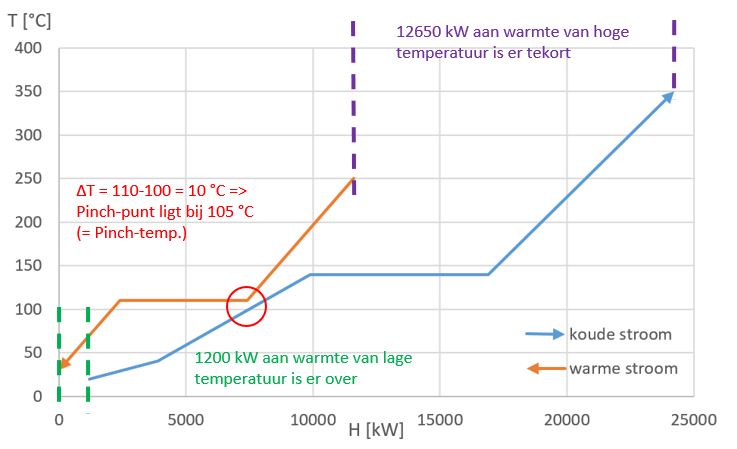
Vervolgens worden beide composite curves in een temperatuur-enthalpiediagram uitgezet, waarna de koude composite curve zodanig in horizontale richting wordt verschoven dat de verticale afstand tussen de twee curves gelijk is aan een vastgesteld minimaal temperatuurverschil voor warmteoverdracht. Een veelgebruikt temperatuurverschil is 10 °C. De temperatuur bij dit minimale temperatuurverschil wordt de Pinch-temperatuur of het Pinch-punt genoemd. Onderstaande figuur laat een voorbeeld zien van composite curves. De hoeveelheid lage-temperatuurwarmte die weggekoeld moet worden, wordt in het Engels "cold utility" of "cooling duty" genoemd. De hoeveelheid hoge-temperatuurwarmte die van buitenaf aan het systeem toegevoerd moet worden, wordt in het Engels "hot utility" of "heating duty" genoemd.
Nadat het bovenstaande gedaan is, kunnen de Pinch-regels toegepast worden:
• voer geen warmte toe bij temperaturen onder de Pinch
• voer geen warmte af boven de Pinch
• wissel geen warmte uit over de Pinch
De enige correcte plaats voor een warmtepomp is over de Pinch. Ofwel, het overschot aan lage-temperatuurwarmte onder de Pinch gebruiken om in het tekort aan hoge-temperatuurwarmte boven de Pinch te voorzien. Bij het voorbeeld in bovenstaande figuur betekent dit dat de warmte met een temperatuur van 110 °C (als Qlaag) door de warmtepomp wordt gebruikt om warmte van 140 °C (Qhoog) te produceren.
Achtergrondinformatie
• Key concepts of Pinch analysisw (boekhoofdstuk)
Brandstofcellen
Bij thermische centrales wordt de warmte die vrijkomt bij de verbranding van een brandstof (aardgas, steenkool, afval) via een stoomcyclus omgezet in elektriciteit. Bij brandstofcellen wordt de elektriciteit niet geproduceerd via warmte, maar vindt directe omzetting plaats van chemische energie in elektriciteit. De essentie van een brandstofcel (en ook van een elektrolyser) is dat er geen rechtstreekse uitwisseling van elektronen plaatsvindt tussen de te reageren stoffen.
Een brandstofcel bestaat eenvoudig gezegd uit twee elektroden, een kathode en een anode, die zich in een elektrolyt bevinden. De overall reactie bij een waterstof/zuurstof-brandstofcel is:
$$ \H_2 + 0,5\O_2 → \H_2\O $$
Deze reactie bestaat uit een tweetal deelreacties bij de anode, resp. de kathode:
$$ \H_2 → 2 \H^{+} + 2 \e^{-} $$
$$ 0,5 \O_2+ 2 \H^{+} + 2 \e^{-} → \H_2\O $$
De ionen (H+) kunnen wel door de elektrolyt stromen, maar de elektronen (e-) niet. De elektronen kunnen alleen via een omweg, een stroomdraad, van anode naar kathode stromen. Het elektronentransport door de stroomdraad houdt in dat er elektriciteit door de stroomdraad gaat.
Brandstofcelrendement en -vermogen
Het maximale, theoretische rendement van een brandstofcel is afhankelijk van de veranderingen in Gibbs energie en enthalpie door de brandstofcelreactie:
$$ η_{\fc,\max} = {\ΔG} / {\ΔH} $$
Dit kan bij constante temperatuur $T$ desgewenst worden omgeschreven tot:
$$ η_{\fc,\max} = {\ΔH - T\ΔS} / {\ΔH} = 1 - T {\ΔS} / {\ΔH} $$
Volgens Au et al. (2002) kan, onder aanname dat de verhouding tussen enthalpie en entropie ongeveer constant is als functie van de temperatuur, de vorige vergelijking worden vereenvoudigd tot:
$$ η_{\fc,\max} = 1 - T / T_{\ΔG=0} $$
Voor de waterstof/zuurstof-reactie geldt: TΔG=0 ≈ 5000 K.
IV-curve
De prestatie van een brandstofcel kan weergegeven worden in de vorm van een zogenaamde IV-curve (O'Hayre (2006)). In de IV-curve is de celspanning (V) uitgezet als functie van de stroomdichtheid. Het rendement van een brandstofcel is rechtevenredig met de celspanning en is dus hoger bij een lagere stroomdichtheid en dus ook hoger in deellastbedrijf.
Aangezien de geproduceerde hoeveelheid elektriciteit afhankelijk is van de grootte van de brandstofcel, is de stroom (I) voor de IV-curve genormaliseerd tot stroomdichtheid. De IV-curve voor een MCFC-brandstofcel waarbij alleen Ohmse verliezen(*) optreden is lineair en ziet eruit als in onderstaande figuur. Naast de IV-curve is in deze figuur ook de vermogensdichtheid uitgezet. De vermogensdichtheid is gelijk aan de celspanning maal de stroomdichtheid, want ook voor het vermogen P van een brandstofcel geldt:
$$ P = U · I $$
De maximale spanning, ook wel thermodynamische open-klemspanning genoemd, die een brandstofcel kan leveren is ook afhankelijk van de verandering in Gibbs energie door de brandstofcelreactie:
$$ U_{\fc,\max} = {-\Δ_{r}g} / {2\F} $$
met:
F = constante van Faraday (96485 Coulomb/mol)
In werkelijkheid is de open-klemspanning lager. En zoals aan de IV-curve te zien is, is de spanning nog weer lager wanneer de brandstofcel stroom levert.
De spanning, en daarmee het vermogen, van een enkele brandstofcel is dus vrij laag. Wanneer brandstofcellen in serie worden geplaatst, een zogenaamde brandstofcelstack, wordt de spanning evenredig groter. Zo zorgen tien brandstofcellen van elk 0,6 V in serie voor een spanning van 6 V. Vermenigvuldigen van deze spanning met de stroom(dichtheid) geeft het vermogen van de brandstofcelstack.
(*) Ohmse verliezen zijn spanningsverliezen als gevolg van de geleidingsweerstand.
Soorten brandstofcellen
Er bestaan verschillende typen brandstofcellen. Het grote verschil is de gebruikte elektrolyt. Enkele brandstofceltypes zijn: SOFC (solid oxide fuel cell), MCFC (molten carbonate fuel cell), PAFC (phosphoric acid fuel cell), PEMFC (polymer electrolyte membrane fuel cell) en AFC (alkaline fuel cell). Een ander verschil is de bedrijfstemperatuur. Deze hangt samen met de gebruikte elektrolyt. De types SOFC en de MCFC behoren tot de hoge-temperatuurbrandstofcellen vanwege een bedrijfstemperatuur van meer dan 200 °C. Ook het gebruikte ion verschilt (H+, OH-, CO32-, O2-).
Interne en externe reforming
Als brandstof voor de brandstofcel wordt waterstof gebruikt. Deze waterstof wordt extern geproduceerd (externe reforming), bijvoorbeeld uit methaan. Een alternatief voor externe reforming is interne reforming. Bij interne reforming wordt de waterstof in de brandstofcel zelf geproduceerd. Bijvoorbeeld de brandstofceltypen SOFC en MCFC kunnen methaan gebruiken als brandstof. Een relatief nieuw type brandstofcel is de DMFC (direct methanol fuel cell) waarbij methanol als brandstof wordt gebruikt.
Ten slotte verschillen brandstofcellen qua toepassingsgebied en vermogen. Een voorbeeld is de toepassing van een brandstofcel in een micro-WKK voor de decentrale (huishoudelijke) productie van elektriciteit en warmtew. Overigens kan niet alleen een brandstofcel gebruikt worden voor een micro-WKK maar kan deze ook aangedreven worden met een Stirlingmotor. In het eerste geval is het hoofdproduct elektriciteit, in het tweede geval is dit warmte.
Brandstofcel gecombineerd met Carnot-motor
De warmte die vrijkomt bij een brandstofcel kan naar een Carnot-motor gevoerd worden voor de productie van elektriciteit. Voor het theoretische rendement van het gecombineerde systeem geldt:
$$ η_s = η_{\fc} + (1 - η_{\fc})η_c $$
Invullen van de reversibele rendementen leidt tot:
$$ η_{\s,\rev} = 1 - T_0 {\ΔS} / {\ΔH} = 1 - {T_0} / {T_{\ΔG=0} $$
Met T0 = 298 K en TΔG=0 ≈ 5000 K volgt uit bovenstaande vergelijking dat het systeemrendement in het reversibele geval ongeveer 94% en onafhankelijk van de bedrijfstemperatuur is.
Door Haynes (2001) wordt ingegaan op de prestaties van brandstofcellen en warmtemotoren. Er wordt beargumenteerd dat het voor een goede vergelijking van belang is rekening te houden met de systeemgrenzen en dat daarom brandstofcellen en warmtemotoren beter vergeleken kunnen worden op basis van respectievelijk een brandstofcelsysteem en een warmtemotor-systeem. Tevens wordt een formule voor het ideale rendement van een brandstofcel geïntroduceerd waarmee een betere vergelijking mogelijk is tussen brandstofcellen met hoge en lage werktemperatuur.
Achtergrondinformatie
• brandstofcellenw (werkingsprincipe en soorten)
• brandstofceltoepassingenw
Elektrolyse
Een elektrolyser (elektrolysecel) is min of meer het omgekeerde van een brandstofcel (accu, galvanische cel): een brandstofcel produceert elektriciteit door waterstof met zuurstof te laten reageren tot water terwijl een elektrolyser elektriciteit gebruikt om water te splitsen in waterstof en zuurstof. Het rendement van een elektrolyser is 70-80%.
Er bestaan verschillende soorten elektrolyers voor waterstofproductie, zoals de alkaline waterelektrolyser en de proton exchange membrane waterelektrolyser. Van deze twee types bestaat de alkaline waterelektrolyser het langst en is daarmee ook het meest ontwikkeld. De nieuwere proton exchange membrane waterelektrolyser heeft als voordeel de mogelijkheid van flexible dynamische operatie waardoor goed ingespeeld kan worden op wisselende beschikbaarheid van elektriciteit. Nadeel van het nieuwere type is het gebruik van kritieke en waardevolle materialen zoals titaan, platina, iridium voor de elektrodes en het benodigde polymeermateriaal voor het membraan. Dit type is hierdoor ook duurder (Bareiß et al., 2019).
Alkaline waterelektrolyser
Bij de alkaline waterelektrolyser (AWE) wordt gewoonlijk een waterige oplossing van kaliumhydroxide (KOH) als elektrolyt gebruikt (Santos et al., 2013). De twee elektrodes worden gescheiden door een poreus diafragma dat wel de hydroxide-ionen (OH-) doorlaat maar niet de gevormde gassen, zodat waterstof en zuurstof van elkaar gescheiden blijven. Onderstaande figuur laat het principeschema van een AWE zien.
De deelreacties die bij de anode, resp. de kathode plaatsvinden zijn:
$$ 2 \OH^{-} → 0,5 \O_2+ \H_2\O + 2 \e^{-} $$
$$ 2 \H_2\O + 2 \e^{-} → \H_2 + 2 \OH^{-} $$
Proton exchange membrane waterelektrolyser
Een proton exchange membrane waterelektrolyser (PEMWE) gebruikt in plaats van een vloeibare elektrolyt een dunne membraan bestaande uit een polymeer als elektrolyt (Bareiß et al., 2019). Onderstaande figuur laat het principeschema inclusief de betreffende reacties zien.
Achtergrondinformatie
• alkaline waterelektrolysew (Santos et al., Hydrogen production by alkaline water electrolysis)
• proton exchange membrane waterelektrolysew (Bareiß et al., Life cycle assessment of hydrogen from ptoton exchange membrane electrolysis in future energy systems))
Energie en eXergie
Energie kan in veel vormen voorkomen, denk aan elektriciteit, warmte, zonne-energie, brandstoffen etc. De ene energievorm is waardevoller dan de andere. Elektriciteit kan bijvoorbeeld vrij gemakkelijk in warmte worden omgezet, andersom is moeilijker, zie hiervoor ook de Carnot-kringloop.
Exergie wordt de ‘kwaliteit van energie’ genoemd en is het nuttige deel van een energiestroom. Het deel van een energiestroom dat niet nuttig is, heeft ook een naam: anergie. Energie bestaat dus uit exergie en anergie, resp. een nuttig en een niet-nuttig deel. Elektriciteit kan volledig nuttig worden ingezet; de exergiewaarde van elektriciteit is gelijk aan de energiewaarde. Elektriciteit heeft een hogere kwaliteit dan warmte. Voor een warmtestroom geldt dat hoe hoger de temperatuur, hoe meer nut die stroom heeft en dus hoe groter de exergiewaarde is, zoals weergegeven in onderstaande figuur. Exergiewaarden worden berekend ten opzichte van een referentieomgeving.
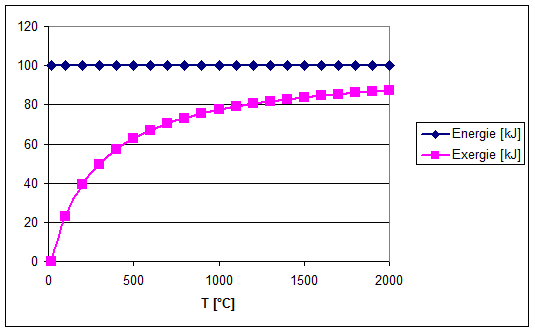
De energie- en exergie-inhoud van 100 kJ warmte als functie van de temperatuur van die warmte. De omgevingstemperatuur is 15 °C.
Volgens de eerste hoofdwet van de thermodynamica gaat energie nooit verloren. De term ‘energieverlies’ is dus niet correct. Wat wel altijd verloren gaat is exergie. Waar bij energieanalyses alleen rekening wordt gehouden met de eerste hoofdwet van de thermodynamica, houdt het exergiebegrip ook rekening met de tweede hoofdwet van de thermodynamica. Volgens deze tweede hoofdwet kan arbeid (elektriciteit) zonder meer in warmte worden omgezet, maar warmte niet zonder meer in arbeid.
Bij elk proces en elke handeling treedt exergieverlies op, met andere woorden: gaat kwaliteit van energie verloren. Voor een deel is dit kwaliteitsverlies onvermijdelijk, maar vaak kan het beperkt worden. Beperken van het kwaliteitsverlies houdt veelal een besparing van grondstoffen en energie in. Kwaliteitsverlies, exergieverlies, wordt niet zichtbaar gemaakt met energieanalyses.
Uit onderstaande figuur blijkt dat de resultaten van energie- en exergieanalyses tot verschillende conclusies kunnen leiden met betrekking tot de te verbeteren secties van een proces. Volgens de resultaten van de energieanalyse heeft de zuiveringssectie van het ICI lage-druk methanolproces namelijk het grootste verbeterpotentieel, maar volgens de exergieanalyse gaat de meeste exergie verloren bij de productie van synthesegas.
Energiegebruik en exergieverliezen in de secties van het ICI lage-druk methanolproces (Stougie (2014)w).
Door Rosen (2006a), Rosen (2006b) en Stougie (2014) wordt ingegaan op de verschillen tussen energie- en exergieanalyse en de voordelen die exergieanalyse voor industrie, overheid en maatschappij heeft op het gebied van energie, milieu en economische ontwikkeling. Voor een analyse van de aarde als geheel en van de subsystemen biosfeer, het menselijke energiesysteem en de menselijke bevolking zelf wordt verwezen naar Rosen and Scott (2003a) en Rosen and Scott (2003b). Door hen wordt o.a. ingezoomd op de waterkrachtcentrales bij de Niagara watervallen, kolengestookte elektriciteitsproductie en verschillende manieren voor ruimteverwarming in huizen, tevens wordt kort ingegaan op brandstofcellen.
Achtergrondinformatie
• website Doe meer met de kwaliteit van energiew (introductie exergie, berekening exergiewaarden, -verliezen etc)
• syllabus Exergieanalysew (o.a. berekening exergiewaarden en -verliezen)
• proefschriftw (Exergy and Sustainability - Insights into the Value of Exergy Analysis in Sustainability Assessment of Technological Systems)
Wat is exergieverlies?
Bij exergieanalyse wordt onderscheid gemaakt tussen intern en extern exergieverlies.
Intern exergieverlies
Het interne exergieverlies is een rechtstreeks gevolg van de tweede hoofdwet van de thermodynamica; elke omzetting of handeling gaat gepaard met exergieverlies. Bij elk proces is de totale hoeveelheid uitgaande exergie altijd minder dan de totale hoeveelheid ingaande exergie, het verschil in exergiehoeveelheid wordt het interne exergieverlies genoemd.
In formulevorm:
$$ Ex_{\verlies,\intern} = \Σ Ex_{\in,\i} - \Σ Ex_{\uit,\j} $$
met:
$Ex_{\in,\i}$ = exergie van ingaande proces- en energiestroom i
$Ex_{\uit,\j}$ = exergie van uitgaande proces- en energiestroom j
Dit interne exergieverlies wordt niet zichtbaar gemaakt met een energieanalyse, immers volgens de eerste hoofdwet van de thermodynamica is de totale hoeveelheid uitgaande energie altijd gelijk aan de totale ingaande hoeveelheid energie. Intern exergieverlies wordt veroorzaakt door drijvende krachten.
Extern exergieverlies
Het externe exergieverlies is de hoeveelheid exergie die het proces verlaat in de vorm van bijvoorbeeld afvalstromen, emissies en warmteverliezen naar de omgeving. Dit zijn dezelfde stromen die bij een energieanalyse tot de verliesstromen worden gerekend. Het enige verschil is dat bij exergieanalyse met de exergie- in plaats van met de energiewaarde van die verliesstromen wordt gerekend.
Oorzaken van intern exergieverlies
Intern exergieverlies wordt veroorzaakt door de drijvende krachten die nodig zijn om processen te laten verlopen, zoals het temperatuurverschil benodigd bij warmtewisseling. Andere voorbeelden van drijvende krachten zijn: verschil in druk, hoogte en concentratie. In het algemeen geldt dat hoe groter de drijvende kracht, hoe sneller het proces verloopt en hoe groter het exergieverlies. Vanuit het oogpunt van exergie ligt het voor de hand om drijvende krachten zoveel mogelijk te verminderen. Of dat in de praktijk haalbaar is, zal van geval tot geval moeten worden bekeken.
Reactoren
Hoe sneller een reactie verloopt en hoe meer warmte er bij de reactie vrijkomt, hoe groter het exergieverlies in de reactor. Verbranding is bijvoorbeeld een reactie die gepaard gaat met een relatief groot exergieverlies. Mogelijkheden om exergieverliezen in reactoren te beperken zijn bijvoorbeeld: het gebruik van brandstofcellen in plaats van ‘gewone’ reactoren, het koppelen van chemische reacties zodat de warmte die vrijkomt bij de ene reactie wordt gebruikt om de andere reactie te laten verlopen, en de inzet van katalysatoren die mildere reactieomstandigheden mogelijk maken.
Turbines en compressoren
Exergieverliezen in turbines en compressoren worden veroorzaakt door wrijving langs de wanden en inwendige lekkage door (noodzakelijke) speling tussen stilstaande en roterende delen binnen het apparaat (Stougie et al. (1997)). Deze verliezen zijn sterk afhankelijk van het ontwerp van de turbine of compressor. Bij een turbine kunnen de verliezen beperkt worden door bij een kleiner vermogen van de turbine voor een lagere stoomdruk aan de inlaat van de turbine te kiezen, vervuiling van het schoepenkanaal tegen te gaan en door maatregelen te nemen om stoomdruppeltjes zo goed mogelijk uit de stoomstroom te verwijderen. Bij een compressor kunnen de exergieverliezen beperkt worden door het vermijden van een hoge uitlaatdruk bij een relatief kleine ingaande volumestroom en het goed schoon houden van de inlaatzijde van het schoepensysteem om wrijvingsverliezen zoveel mogelijk te beperken.
Warmtewisselaars
Hoe groter het temperatuurverschil tussen de op te warmen en af te koelen stroom, hoe groter het exergieverlies. Zo is het exergieverlies bij een meestroomwarmtewisselaar groter dan bij een tegenstroomwarmtewisselaar.
Berekening van exergiewaarden
De exergiewaarde van een stof of stroom wordt bepaald ten opzichte van een referentieomgeving. Hoe meer de stof of stroom qua samenstelling en condities (bijvoorbeeld druk en temperatuur) verschilt van de referentieomgeving, hoe hoger de exergiewaarde van die stof of stroom.
Exergie is gedefinieerd als de maximale hoeveelheid arbeid die verkregen kan worden wanneer een stof of stroom in evenwicht wordt gebracht met de (referentie)omgeving.
Een aantal energievormen heeft zo’n hoge kwaliteit dat de exergiewaarde gelijk is aan de energiewaarde van de stof of stroom. Dit geldt bijvoorbeeld voor elektriciteit en kinetische en potentiële energie. Ook voor brandstoffen als aardgas en benzine geldt dat de exergiewaarde nagenoeg gelijk is aan de energiewaarde (stookwaarde).
Referentieomgeving
De referentieomgeving is qua samenstelling en condities een afspiegeling van de aarde en bestaat uit componenten zoals die voorkomen in de lucht, de oceanen en de aardkorst. Er bestaan verschillende modellen voor de referentieomgeving.
Exergiewaarde van massastromen
De exergiewaarde van massastromen is opgebouwd uit een fysische en een chemische component. De fysische component, ook wel de thermomechanische exergie van een massastroom genoemd, is de maximale hoeveelheid arbeid die verkregen kan worden wanneer de massastroom qua druk en temperatuur in evenwicht wordt gebracht met de referentieomgeving, zie onderstaande vergelijking. Er is dan sprake van thermomechanisch evenwicht. Onderstaande vergelijking is vrij eenvoudig af te leiden uit het toepassen van de eerste en tweede hoofdwet op een open systeem.
$$ {Ex}_{\m,\fys} = φ_\m ((H - H_0) - T_0(S - S_0)) $$
met:
$Ex_{\m,\fys}$ = fysische exergiewaarde van een massastroom [J/s]
$φ_\m$ = massastroom [kg/s]
$H$, $H_0$ = enthalpiewaarde massastroom in begin- resp. omgevingstoestand [J/kg]
$S$, $S_0$ = entropiewaarde massastroom in begin- resp. omgevingstoestand [J/kgK]
$T_0$ = temperatuur referentieomgeving [K]
De chemische exergiewaarde van een massastroom is gelijk aan de maximale hoeveelheid arbeid die verkregen kan worden wanneer de massastroom van thermomechanisch evenwicht in volledig evenwicht met de referentieomgeving wordt gebracht. Bij volledig evenwicht heeft de massastroom de druk en temperatuur van de referentieomgeving aangenomen en zijn de stoffen waaruit de massastroom bestaat, omgezet in stoffen zoals die voorkomen in de referentieomgeving.
Een van de manieren om de chemische exergiewaarde van stoffen te berekenen is uitgaande van de standaard chemische exergiewaarden van de elementen en de vorming van de betreffende stof uit die elementen, zoals weergegeven in onderstaande vergelijking:
$$ ex_{\ch,i}^0(T_0) = Δ_{\f}g_{i}^0(T_0) + Σ(N_e ex_{\ch,e}^0(T_0)) $$
met:
$ex_{\ch,i}^0(T_0)$ = standaard chemische exergiewaarde stof i bij $T_0$ [J/mol]
$ex_{\ch,e}^0(T_0)$ = standaard chemische exergiewaarde element e bij $T_0$ [J/mol]
$Δ_{\f}g_{i}^0(T_0)$ = molaire Gibbs vormingsenergie stof i bij $T_0$ [J/mol]
$N_e$ = aantal mol van element e per mol i [-]
Exergiewaarde van warmtestromen
Bij de introductie van het begrip exergie is reeds behandeld dat de exergiewaarde van een warmtestroom berekend kan worden door de energiewaarde te vermenigvuldigen met de Carnot-factor. Voor de lage temperatuur wordt dan de temperatuur van de referentieomgeving gebruikt en de hoge temperatuur is uiteraard gelijk aan de temperatuur van de warmtestroom zelf. Wanneer de 'warmte'stroom een lagere temperatuur heeft dan de referentieomgeving dan moet de absolute waarde van de Carnot-factor genomen worden.
Bij het berekenen van de exergiewaarde van een warmtestroom waarvan de temperatuur verandert (bijvoorbeeld in een warmtewisselaar), wordt voor de temperatuur de thermodynamisch gemiddelde temperatuur genomen.
Weergave van de resultaten van exergieanalyses
Er zijn verschillende manieren om de resultaten van exergieanalyses weer te geven, bijvoorbeeld grafisch in de vorm van Grassmann- of waardediagrammen of door het berekenen van rendementen.
Grassmann-diagram
Het Grassmann-diagram is het equivalent van het Sankey-diagram bij energieanalyses. De breedtes van de getekende stromen in het diagram zijn een maat voor de exergiewaarden van die stromen.
Waardediagram
In een waardediagram worden de exergieverliezen zichtbaar gemaakt als oppervlaktes in het diagram. Op de horizontale as wordt de warmtehoeveelheid uitgezet en op de verticale as de bijbehorende temperatuur T in de vorm van 1-T0/T. De verticale as loopt van 0 tot 1.
Onderstaande figuur is een voorbeeld van een waardediagram. Het totale oppervlak van de figuur is gelijk aan de exergie-inhoud van de brandstof. Het oppervlak onder de afkoelkromme is gelijk aan de exergie-inhoud van de warmte die is vrijgekomen door de verbranding. Het gearceerde oppervlak is het exergieverlies veroorzaakt door de verbranding.
.
Universeel rendement
Het universele rendement is gedefinieerd als:
$$ η_{\Ex,\univ} = { \Σ Ex_{\uit,\j} } / { \Σ Ex_{\in,\i} } $$
met:
$Ex_{\in,\i}$ = exergie van ingaande proces- en energiestroom i
$Ex_{\uit,\j}$ = exergie van uitgaande proces- en energiestroom j
Het universele rendement heeft als nadeel dat de gevoeligheid van het rendement sterk afhangt van de grootte van de in- en uitgaande stromen, zoals behandeld bij de definities van rendementen.
Functioneel rendement
Bij het functionele rendement wordt onderscheid gemaakt tussen ‘essentiële’ en ‘ballast’stromen (Woudstra (1995)). Met ‘ballaststromen’ worden exergiestromen bedoeld die aan het proces toegevoerd worden maar niet direct betrokken zijn bij de beoogde omzetting. Het functionele rendement is gedefinieerd als:
$$ η_{\Ex,\func} = { \Σ Ex_{\product,\j} } / { \Σ Ex_{\bron,\i} } $$
met:
$Ex_{\bron,\i}$ = exergie van dat deel van ingaande proces- en energiestroom i dat bij het beschouwde proces als noodzakelijk voor het tot stand komen van het product kan worden aangemerkt
$Ex_{\product,\j}$ = exergie van dat deel van uitgaande proces- en energiestroom j dat als product van het systeem kan worden aangemerkt
Nadeel van het functionele rendement is dat er per systeem vastgesteld zal moeten worden welke stromen tot de product- en bronstromen behoren. Door Woudstra (1995) is dit voor een groot aantal apparaten gedaan, waaronder voor turbines, condensors, pompen, warmtewisselaars, compressoren. Het functionele exergierendement van een warmtewisselaar is bijvoorbeeld gedefinieerd als de exergie opgenomen door de opwarmende stroom gedeeld door de exergie afgegeven door de afkoelende stroom. In formulevorm:
$$ η_{\Ex,\func,\ww} = { Ex_{\opwarmende \stroom, \uit} - Ex_{\opwarmende \stroom, \in} } / { Ex_{\afkoelende \stroom,\in} - Ex_{\afkoelende \stroom,\uit} } $$
Zonne-energie
De zonnestraling die de aarde bereikt bestaat grotendeels uit zichtbaar licht en deels uit infrarood (warmtestraling) en UV-straling. Zonne-energie kan vastgelegd worden door fotovoltaïsche (zon-PV) en zon-thermische installaties.
Zon-PV
Bij fotovoltaïsche (photovoltaïsche, PV-) installaties wordt gebruik gemaakt van een combinatie van halfgeleiders om zonne-energie om te zetten in elektriciteit. Het zonlicht zorgt ervoor dat een elektron in een zogenoemde aangeslagen toestand raakt. Om ervoor te zorgen dat zo’n aangeslagen elektron maar een kant op kan gaan en er stroom gaat lopen, wordt gebruik gemaakt van twee typen halfgeleiders.
Onderstaande figuur laat zien dat instraling van licht ervoor zorgt dat een elektron uit het p-type halfgeleider zich verplaatst naar het n-type geleider. Het elektron kan niet terug van het n-type naar het p-type geleider. Het gat (h+) dat het elektron achterlaat in het p-type geleider kan weer opgevuld worden door een ander elektron in het p-type geleider. Wanneer beide geleiders worden opgenomen in een elektrisch circuit, zal er een elektrische stroom gaan lopen op het moment dat er zonlicht op het p-type halfgeleider schijnt.
Een p-type halfgeleider ontstaat door aan een halfgeleidend materiaal een verontreiniging toe te voegen (‘te doteren’) die een elektron minder in de valentieschil heeft, bijvoorbeeld door gallium (Ga) of indium (In) toe te voegen aan silicium (Si). Het resterende materiaal heeft een tekort aan elektronen. Er wordt ook wel gezegd dat dit materiaal positieve deeltjes of ‘positief geladen gaten’ heeft. Andersom ontstaat een n-type halfgeleider door een verontreiniging te doteren die een elektron meer in de valentieschil heeft, bijvoorbeeld door arseen (As) of antimoon (Sb) toe te voegen aan silicium. Een n-type halfgeleider heeft een overschot aan elektronen.
Het maximale rendement van een zonnepaneel is gedefinieerd als:
$$ η_{\max} = P_{\max}/P_{\zonlicht} $$
met:
$P_{\max}$ = maximaal vermogen van een zonnepaneel, ofwel het aantal Wattpiek (Wp)
$P_{\zonlicht}$ = ingestraald vermogen van de zon
Het maximale vermogen van een zonnepaneel (of zonnecel) gemeten bij standaardomstandigheden, waaronder 1000 W/m2 aan invallende zonnestraling en bij een temperatuur van 25 °C van zonnecel/zonnepaneel, wordt uitgedrukt in Watt peak (Wp, ‘Wattpiek’). Het werkelijke vermogen van een zonnepaneel is o.a. afhankelijk van de locatie van het zonnepaneel, de oriëntatie ten opzichte van de zon en de hellingshoek waaronder het paneel geplaatst is.
Volgens Milieucentraal (2014) gaan zonnepanelen zeker 25 jaar mee en heeft een zonnesysteem na 3 jaar elektriciteitsproductie evenveel elektriciteit opgewekt als er aan energie nodig was bij de productie van het systeem.
Zon-thermisch
Bij zon-thermische installaties wordt zonne-energie gebruikt om een vloeistof, meestal water, op te warmen. Voorbeelden van zon-thermische installaties zijn zonneboilers op de daken van huizen en bedrijfspanden, en grootschalige zonnecentrales waarbij zonlicht met behulp van spiegels geconcentreerd wordt, de zogenaamde Concentrated Solar Power (CSP) installaties.
Er bestaan verschillende uitvoeringsvormen van zonneboilers. Een standaard zonneboiler bestaat uit een collector en een groot opslagvat dat naverwarmd kan worden door een CV-ketel. Bij de compacte zonneboiler is het voorraadvat geïntegreerd in de collector op het dak. Een zonneboilercombi bestaat uit meerdere collectoren en een groot opslagvat en is geschikt voor zowel warm tapwater als verwarmingsdoeleinden door middel van vloer- of wandverwarming. Ook bestaan er verschillende uitvoeringsvormen van de collector, namelijk een vlakke plaat of (nieuwer) collectorbuizen.
Bij grootschalige zonnecentrales kan zonlicht geconcentreerd worden door middel van parabolische trogspiegels, lineaire Fresnel-spiegels, zonnetorens en parabolische schotelspiegels, zie onderstaande figuren. Met uitzondering van de parabolische schotelspiegels wordt de opgevangen zonnewarmte vervolgens gebruikt om een Rankine-cyclus aan te drijven. Een parabolische schotelspiegel wordt gecombineerd met een Stirling-cyclus.
De parabolische trogspiegel wordt het meest toegepast. De rijen spiegels zijn in noord/zuid-richting geplaatst en draaien mee met de zon als die van oost naar west gaat. Het zonlicht wordt met behulp van de trogspiegels geconcentreerd en gebruikt om het transportmedium in de lange buis tot ca. 550 °C te verhitten. Oorspronkelijk was dit medium een soort olie, maar tegenwoordig wordt hiervoor gesmolten zout (een mengsel van natrium- en kaliumnitraat) gebruikt. Het hete zoutmengsel wordt gebruikt om water om te zetten in stoom. Wanneer het gesmolten zout in speciale opslagtanks wordt opgeslagen kan het tot zo'n zes uur zijn warmte behouden en daarmee gebruikt worden om een periode zonder zon te overbruggen.
Frensnel-spiegels zijn vlak of licht gebogen, draaien over een as en concentreren het zonlicht naar een meer van de ontvangers boven de spiegels. Deze technologie is kostenbesparend ten opzichte van trogspiegels en schotelspiegels doordat er één ontvanger voor een aantal spiegels gebruikt wordt.
Bij een zonnetoreninstallatie draaien de spiegels op de grond om twee assen zodat er gedurende meer uren per dag zo veel mogelijk zonlicht opgevangen kan worden. De spiegels concentreren het zonlicht naar een ontvanger bovenin de toren die de warmte overdraagt naar een transportmedium, gewoonlijk gesmolten zout. Het zout kan worden opgeslagen voor toekomstig gebruik of zijn warmte overdragen naar een verzadigd stoomsysteem.
Bij een parabolische schotelspiegel wordt geen stoomcyclus toegepast, maar wordt een Stirling-motor aangedreven. De schotelspiegels draaien om twee assen waardoor de zon dagelijks van oost naar west en met de seizoenen mee ook van noord naar zuid en vice versa gevolgd kan worden. Het rendement van een parabolische schotelspiegel bedraagt ca. 30% en is daarmee aanzienlijk hoger dan het rendement van de andere types CSP-installaties (15-20%).
Achtergrondinformatie
• werking zonnepanelenw (website Milieucentraal)
• werking zonneboilerw (website Milieucentraal)
• CSP-installatiesw (beschrijving verschillende types)
• overzicht operationele CSP-installatiesw
• Ivanpah Solar Electric Generating Systemw
• Solaben CSP-installatiew
• artikel Energy intensities, EROIs (energy returned on invested), and energy payback times of electricity generating power plantsw (Weißbach et al. (2013), alleen vanaf TU-netwerk!)
Bronnen
Au et al. (2002), Au, S.F., K. Hemmes and N. Woudstra (2002). The Influence of Operating Temperature on the Efficiency of Combined Fuel Cell and Power Cycle System. Journal of the Electrochemical Society 149(7): A879-A885Bareiß et al., 2019, Bareiß, K., C. de la Rua, M. Möckl, T. Hamacher (1999). Life cycle assessment of hydrogen from proton exchange membrane electrolysis in future energy systems. Applied Energy 237:862-872
Dijkema et al. (2009), Dijkema, G., Z. Lukszo, A. Verkooijen, L. de Vries en M. Weijnen (2009). De regelbaarheid van elektriciteitscentrales
Haynes (2001), Haynes, C. (2001). Clarifying reversible efficiency misconceptions of high temperature fuel cells in relation to reversible heat engines. Journal of Power Sources 92: 199-203
Milieucentraal (2014), Milieucentraal. (2014). http://www.milieucentraal.nl/thema%27s/thema-1/energie-besparen/zonnepanelen/hoe-werken-zonnepanelen/ geraadpleegd op 13 oktober 2014
Moran & Shapiro, Moran, M.J. and H.N. Shapiro (n.d.). Fundamentals of Engineering Thermodynamics, Wiley and Sons, Inc.
O'Hayre (2006), O'Hayre, R.P., et al. (2006). Fuel Cell Fundamentals, John Wiley & Sons, Inc.
Perry and Green (2008), Perry, R.H. and D.W. Green (2008). Perry's Chemical Engineers' Handbook, McGraw-Hill
Rosen (2006a), Rosen, M.A. (2006a). Benefits of exergy and needs for increased education and public understanding and applications in industry and policy: Part I - Benefits. International Journal of Exergy 3(2): 202-218
Rosen (2006b), Rosen, M.A. (2006b). Benefits of exergy and needs for increased education and public understanding and applications in industry and policy: Part II - Needs. International Journal of Exergy 3(2): 219-229
Rosen and Scott (2003a), Rosen, M.A. and D.S. Scott (2003a). Entropy production and exergy destruction: Part I - Hierarchy of Earth's major constituencies. International Journal of Hydrogen Energy 28: 1307-1313
Rosen and Scott (2003b), Rosen, M.A. and D.S. Scott (2003b). Entropy production and exergy destruction: Part II - illustrative technologies. International Journal of Hydrogen Energy 28: 1315-1323
Santos et al., 2013, Santos, D.M.F., C.A.C. Sequeira, J.L. Figueiredo (2013). Hydrogen production by alkaline water electrolysis. Quim. Nova 36(8):1176-1193
Smith & Van Ness, Smith, Van Ness et al. (n.d.). Introduction to Chemical Engineering thermodynamics, McGraw-Hill
Stougie (2014), Stougie, L. (2014). Exergy and Sustainability - Insights into the Value of Exergy Analysis in Sustainability Assessment of Technological Installations. proefschrift, TU Delft
Stougie et al. (1997), Stougie, L., G. C. J. Bart, H. J. van der Kooi, H. van der Ree, N. Woudstra en T. Woudstra (1997). Syllabus Exergie-analyse, TU Delft, Interduct
TU Delft (n.d.), TU Delft (n.d.) Reference guide Cycle-Tempo
Weißbach et al. (2013), Weißbach D., G. Ruprecht, A. Huke, K. Czerski, S. Gottlieb en A. Hussein (2013). Energy intensities, EROIs (energy returned on invested), and energy payback times of electricity generating power plants. Energy 52: 210-221
Woudstra (1995), Woudstra, N. (1995). Exergetische rendementen, TU Delft
Woudstra (2012), Woudstra, N. (2012) Sustainable energy systems: limitations and challenges based on exergy analysis. proefschrift, TU Delft