Instationair warmtetransport

Als de omgevingstemperatuur van een voorwerp verandert, zal ook de temperatuur van het voorwerp gaan veranderen. Als je bijvoorbeeld een ei in kokend water legt, gaat de temperatuur in het ei stijgen. Maar hoe hoger de temperatuur in het ei wordt, des te lager wordt de warmtestroom, want het temperatuurverschil dat de warmteoverdracht veroorzaakt, wordt kleiner. Het warmtetransport is dus tijdsafhankelijk.

Eenzijdige opwarming: indringdiepte

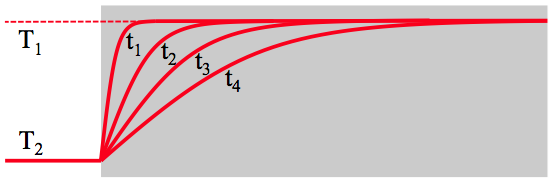
Wanneer een voorwerp aan één kant in contact komt met een hogere temperatuur, zal warmte het voorwerp gaan indringen. In figuur 1 is het proces getekend: links staat de beginsituatie, met $T_1$ de begintemperatuur van het voorwerp en $T_2$ de temperatuur waarmee het in contact wordt gebracht. In de loop van de tijd (steeds latere tijden $t_1$, $t_2$ enz.) zal de temperatuur in het voorwerp oplopen (rechts).


Het effect van de hogere temperatuur zal steeds dieper in het voorwerp merkbaar zijn. Als we een raaklijn tekenen langs de temperatuurkromme bij het oppervlak van het voorwerp, kunnen we bepalen waar deze de lijn van de begintemperatuur ($T_1$) snijdt - zie figuur 2.


De afstand van het oppervlak tot dit punt wordt steeds groter naarmate het voorwerp verder opwarmt. Deze afstand, de "indringdiepte", kunnen we gebruiken als een maat voor hoever de warmte is ingedrongen. De indringdiepte neemt als volgt toe met de tijd:
$$x_i = √{πat}$$
Hierin is $a$ de temperatuurvereffeningscoëfficiënt: $a = λ/{ρc_p}$.
Op de plaats van de indringdiepte is de temperatuur toegenomen met 21% van het temperatuurverschil $T_2-T_1$.

Klik hier voor een simulatie^w van eenzijdige opwarming (klik op START).
Deze simulatie is geldig totdat de warmte de rechter rand bereikt.

Afkoeling

Als een voorwerp juist aan een koudere temperatuur $T_2$ wordt blootgesteld, stroomt de warmte het voorwerp uit. De grafieken zijn dan precies omgekeerd - zie figuur 3 en deze simulatie^w.

Opwarming of afkoeling rondom

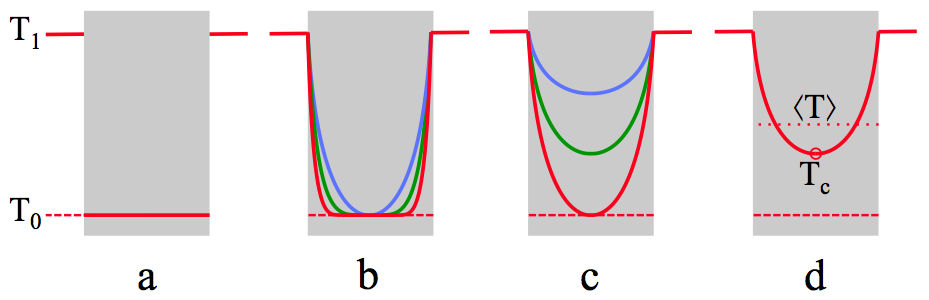
Als een voorwerp aan alle kanten aan een andere temperatuur wordt blootgesteld, verandert de temperatuur aan alle kanten. Figuur 4 laat de opwarming zien van een plaat die in een omgeving komt met aan beide oppervlakken (links en rechts in de figuur) een hogere temperatuur.


Figuur 4a laat de beginsituatie zien: de plaat heeft begintemperatuur $T_0$, de omgeving heeft temperatuur $T_1$. Figuur 4b toont de temperatuur op opeenvolgende tijdstippen in rood, groen en blauw. Op het moment van de blauwe kromme wordt het effect van de temperatuurstijging ook in het centrum van de plaat merkbaar. Daarna gaat ook de centrumtemperatuur $T_c$ stijgen. Dit is weergegeven in figuur 4c, met achtereenvolgende tijdstippen opnieuw in rood, groen en blauw.

Onderstaande simulaties laten zien dat de snelheid in het begin van het proces (figuur (b) hierboven) veel sneller gaat dan later (figuur (c) hierboven). Dit komt doordat de temperatuurgradiënt aan de rand steeds lager wordt, waardoor de warmtestroom steeds kleiner wordt.
• Simulatie van tweezijdige opwarming van een vlakke plaat^w (klik op START)
• Simulatie van tweezijdige afkoeling van een vlakke plaat^w (klik op START)

Grafische methode

De differentiaalvergelijking voor tijdsafhankelijk warmtetransport binnen voorwerpen, zoals de plaat in het voorbeeld, kan voor simpele geometrieën (bollen, cilinders e.d.) analytisch worden opgelost, maar dit is niet eenvoudig. Door gebruik te maken van dimensieloze groepen kan de oplossing echter voor zeer uiteenlopende situaties in grafieken weergegeven worden: TPDC-91+92.

Deze grafieken geven de centrumtemperatuur $T_c$ (TPDC-91) en de gemiddelde temperatuur $⟨T⟩$ (TPDC-92) (zie ook tekening (d) hierboven) als functie van de tijd.

In de grafieken is de tijd dimensieloos gemaakt met de temperatuurvereffeningscoëfficiënt en de karakteristieke afmeting van het voorwerp $d$. Het resultaat is het kental van Fourier, $Fo$:
$${Fo} = {at}/d^2$$ De temperatuur is dimensieloos gemaakt door het verschil tussen de temperatuur in het voorwerp ($T$) en dat van de omgeving ($T_1$) te delen door de waarde van dit temperatuurverschil aan het begin van het proces ($T_0-T_1$):
$$M = {T – T_1}/{T_0 – T_1}$$
Als we bijvoorbeeld een ei willen koken, moet de temperatuur overal in het ei een bepaalde tijd hoger zijn dan 68 °C, om de eiwitten te laten stollen. Nu zal de temperatuur in het centrum van het ei het laatst gaan stijgen. We moeten dus weten na hoelang die temperatuur 68 °C geworden is, want dan is de temperatuur in de rest van het ei zéker hoger. We kunnen dus invullen:

• $T_0$ = 20 °C (begintemperatuur van het ei)
• $T_1$ = 100 °C (temperatuur van het kokende water)
• $T$ = 68 °C (centrumtemperatuur waarvoor willen bepalen wanneer deze optreedt)

Er geldt nu dus: $M = {68-100}/{20-100} = 0,4$.

In de grafiek voor de centrumtemperatuur kunnen we nu aflezen bij welke waarde van $Fo$ deze waarde van $M$ optreedt, en daaruit kunnen we de tijdsduur berekenen. De grafieken bevatten geen eivormige voorwerpen, dus we zullen het moeten doen met een bol als modelvoorwerp. Eventueel kunnen we de berekening herhalen met een cilinder, om een idee te krijgen van het verschil.

Voorwaarde

De voorwaarde om de Fourier-grafiek te mogen toepassen, is dat de temperatuur op de rand van het voorwerp constant moet zijn. In het geval van het ei in het kokende water mogen we dat wel aannemen, want het borrelende water zorgt voor een goede warmteoverdracht.

Blokken en cilinders met H≠D

Voor combinaties van ruimtelijke begrenzingen geldt, dat $M_c$ gelijk is aan het product van de $M_c$’s die horen bij de verschillende ruimtelijke begrenzingen.

Een paar voorbeelden om de voorgaande cryptische zin te verduidelijken:
1. $M_c$ voor een blok met lengte $L$, breedte $B$ en hoogte $H$ is gelijk aan het product van de $M_c$’s voor drie vlakke platen, namelijk met diktes $L$, $B$ en $H$.
2. $M_c$ voor een cilinder met diameter $D$ en lengte $L$ wordt gevonden door $M_c$ voor een oneindig lange cilinder (met diameter $D$) te vermenigvuldigen met $M_c$ voor een vlakke plaat (met dikte $L$).
3. Voor een kubus (waarvan de lijn ook afzonderlijk in de centrum-grafiek gegeven is), zou $M_c$ dus ook berekend kunnen worden uit $M_{c,p}^3$, met $M_{c,p}$ gelijk aan $M_c$ voor een vlakke plaat met een dikte gelijk aan de ribbe van de kubus.

Op dezelfde manier kunnen gemiddelde temperaturen bepaald worden:
1. in een blok met afmetingen $L$, $B$ en $H$: $⟨M⟩_{blok}$ = $⟨M⟩_L⟨M⟩_B⟨M⟩_H$;
2. in een cilinder met afmetingen $D$ en $L$: $⟨M⟩_{cil} = ⟨M⟩_{cil,D}⟨M⟩_{plaat,L}$.

Isolatielaag

Met een trucje kunnen we de grafieken ook gebruiken voor doordringing in een laag die aan één zijde geïsoleerd is (zie figuur 5). In de bovenste figuur dringt warmte van links in, en is er aan de rechterkant een isolatielaag. Dan is de afgeleide van het temperatuurprofiel aan de rechterkant nul, want er is geen warmtetransport. In de onderste figuur is linkerhelft gelijk aan die in de bovenste figuur, en is de temperatuurgradiënt op dezelfde positie nul. Voor het warmtetransportproces in het linkerdeel maakt het dus niet uit welke van beide situaties er in werkelijkheid is. We kunnen de bovenste situatie dan ook modelleren zoals de onderste. (Let op: in dat geval moet voor de lengteschaal de nieuwe, dubbele dikte worden ingevuld.)

Vraagstukken

Asbest

"When John entered the empty room, he found a hot iron on an asbestos plate of 1 cm thickness. He lifted the plate which proved still to be cold on the underside. He decided that somebody had been in the room less than 5 minutes ago and ordered his men to search the apartment." [uit: Beek, Muttzall & van Heuven, Transport Phenomena^w]
Laat zien dat John gelijk heeft.

Spinazie

Conservenblikken met spinazie, met een begintemperatuur van 20 °C, worden in een autoclaaf met stoom van 120 °C gezet om de spinazie te steriliseren. De blikken hebben een diameter en een hoogte van 12 cm. Voor de blikinhoud geldt: $ρ$ = 1200 kg/m³; $λ$ = 0,70 W/m/K; $c_p$ = 4,0 kJ/kg/K. Verwaarloos de warmteweerstand in het metaal ‘blik’ zelf.
a. Schets de temperatuurverdeling in en om het blik op het moment dat de temperatuur in het midden van de blikinhoud net gaat stijgen.
b. Hoe lang moeten de blikken in de autoclaaf staan als alle spinazie een temperatuur van minimaal 110 °C moeten hebben gekregen?
(naar een opgave uit 200 vraagstukken FT^w)

Theeglas

In een theeglas, dat een begintemperatuur van 20 °C heeft, wordt thee van 80 °C geschonken. Het glas heeft een dikte van 3,0 mm en een temperatuursvereffeningscoëfficiënt ($a$) van 4,0·10^-6 m²/s. Neem aan dat voor de beginperiode de lucht als een isolator mag worden beschouwd en de temperatuur van de thee niet daalt.
a. Na hoeveel tijd is de temperatuur van de buitenkant van het glas gestegen tot 75 °C? (Dit is de temperatuur die de huid nog net gedurende 4 seconden kan verdragen.)
b. Als de glas twee keer zo dik zou zijn, hoe verandert dan de tijd totdat de buitenkant een bepaalde temperatuur bereikt heeft?

Kubus

Een kubus (inhoud 1,0 liter) koelt af, waarbij de warmteweerstand geheel binnen de kubus ligt. Na een bepaalde tijd is het verschil tussen de temperatuur in het centrum van de kubus en die van de omgeving een factor 10 afgenomen. Als dezelfde hoeveelheid materiaal niet een kubus- maar een bolvorm had gehad, hoeveel langer (in %) zou de afkoeltijd dan geweest zijn?

Tentamenvraagstuk

Bolletje (a en b; c is voor later bij stoftransport) - Boom - Wand

TB241E

Hoofdpagina
College-index
Thematische index
Alles op één pagina
Laatst gewijzigd
Colofon

Op deze pagina: