Macroscopische impulsbalans

We kunnen de tweede wet van Newton^w:
$$F↖{→} = m·a↖{→}$$ ook schrijven als:
$$F↖{→} = m·{dv↖{→}}/{dt} = {d(mv↖{→})}/{dt}$$ (De pijlen geven aan dat kracht, versnelling en snelheid vectoren zijn.)
Zo bekeken, kunnen we kracht opvatten als veroorzaker van een verandering van $mv↖{→}$ in de tijd. Deze combinatie van massa en snelheid, $mv↖{→}$, heeft in de natuurkunde de naam impuls gekregen, met als symbool $p↖{→}$, dus:
$$F↖{→} = {dp↖{→}}/{dt}$$ Omdat impuls een vector is, moeten we altijd naar drie componenten kijken: $p↖{→} = (p_x, p_y, p_z)$.

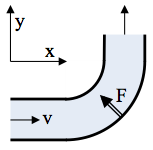
Als in een waterleiding een bocht zit, moet de leiding een kracht uitoefenen op het water om dit de bocht te laten maken. Met een impulsbalans kunnen we uitrekenen hoe groot te kracht is die hiervoor nodig is. We gaan impulsbalansen opstellen voor de bocht in figuur 1.
Eerst kijken we naar de impuls in de x-richting, $p_x$. De algemene vorm voor de impulsbalans in de x-richting is:
$${dp_x}/{dt} = Φ_{p,x,in} - Φ_{p,x,uit} + F_x$$ waarin $Φ_{p,x,in}$ en $Φ_{p,x,uit}$ de ingaande en uitgaande impulsstroom zijn, en $F_x$ de kracht die in de x-richting door de buis op het water wordt uitgeoefend.

Het water stroomt de buis binnen met een gemiddelde snelheid $v$, geheel in de x-richting, dus $v_{x,in} = v$. Daarmee stroomt ook impuls in de x-richting de bocht in: per seconde stroomt $Φ_m$ aan massa binnen, die de snelheid $v_{x,in}$ heeft, dus per seconde is de instroom van impuls in de x-richting gelijk aan $(Φ_m·v)_{x,in} = Φ_m·v$. De uitgaande stroom heeft géén impuls in de x-richting, dus $Φ_{p,x,uit} = 0$. Daarmee wordt de impulsbalans:
$${dp_x}/{dt} = Φ_m·v - 0 + F_x$$ De totale impuls van het water in de bocht blijft steeds gelijk, want de snelheden veranderen niet. Er is wel telkens nieuw water in de bocht, maar de totale impuls blijft hetzelfde. De linker term, ${dp_x}/{dt}$, is dus gelijk aan nul. Ofwel: $0 = Φ_m·v - 0 + F_x$. Daarmee kunnen we de kracht in de x-richting bepalen: $ F_x = -Φ_m·v$.
Op dezelfde manier kunnen we voor de y-richting afleiden:
$${dp_y}/{dt} = Φ_{p,y,in} - Φ_{p,y,uit} + F_y$$ $$0 = 0 - Φ_m·v + F_y$$ Dus geldt: $F_y = Φ_m·v$.
Voor de totale kracht die de buis op het water uitoefent, geldt dus:
$$F_{tot} = √{F_x^2+F_y^2} = √{(-Φ_m·v)^2 + (Φ_m·v)^2$$

Zie ook

Microscopische impulsbalans

Vraagstukken

Bocht

Door een bocht in een leiding stroomt 250 liter water per seconde. De leiding heeft een diameter van 40 cm. De hoek tussen de beide delen van de leiding is 120°.
a. Hoeveel bedraagt de kracht die het water op de leiding uitoefent?

b. Als dit teveel zou zijn voor de constructie, zou de diameter van de leiding dan groter of kleiner gemaakt moeten worden?

Bak

Een bak op wielen met een gewicht van 20 kg wordt horizontaal getroffen door een waterstraal met een diameter van 3,0 cm en een snelheid van 5,0 m/s.
a. Met welke versnelling zal de bak aanvankelijk gaan rollen als de wrijving verwaarloosd mag worden?
b. Hoe komt het dat de versnelling van de bak zal gaan afnemen?

Graan

Uit een voorraadsilo valt per seconde 10 kg graan op een lopende band. Het graan valt, met een te verwaarlozen beginsnelheid, 2,0 m voordat het de band raakt.
a. Met welke snelheid raakt het graan de band?
De band loopt met een snelheid van 1,0 m/s omhoog met een hoek van 30° met de horizontaal.
b. Leid met behulp van een impulsbalans af welke kracht in horizontale richting op het graan moet worden uitgeoefend.
c. Doe hetzelfde voor de verticale richting.

Tentamenvraagstukken

Brielse Meerleiding - Knik - Modder (1) - Opspuiten

TB241E

Hoofdpagina
College-index
Thematische index
Alles op één pagina
Laatst gewijzigd
Colofon

Op deze pagina: