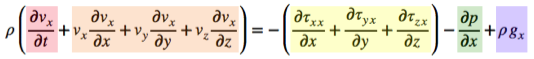Microscopische impulsbalans
Nu we weten hoe een impulsbalans voor een volume moet worden opgesteld, en hoe impuls binnen een fluïdum getransporteerd wordt, kunnen we op heel kleine schaal gaan kijken naar de krachten die spelen in stromingen.
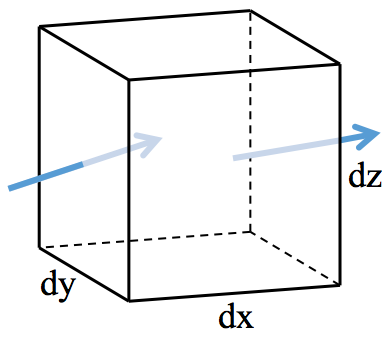
Daarvoor bakenen we in een stroming een kubusvormig volume af met afmetingen dx, dy en dz (zie figuur 1).
Figuur 1. Kubusvormig controlevolume.
$${dp_x}/{dt} = Φ_{p,x,in} - Φ_{p,x,uit} + F_x$$ De term $F_x$ staat voor alle krachten die op het fluïdum in de kubus werken. Dit zijn: de zwaartekracht $F_g$, de kracht $F_p$ ten gevolge van drukverschillen in het fluïdum, en de kracht $F_s$ ten gevolge van snelheidsgradiënten in het fluïdum - allemaal voor zover deze in de x-richting staan. Zo wordt de formule:
$${dp_x}/{dt} = Φ_{p,x,in} - Φ_{p,x,uit} + F_{s,x} + F_{p,x} + F_{g,x}$$ Als de dichtheid van het fluïdum constant is, en dus de massa binnen de kubus ook, geldt:
$${dp_x}/{dt} = {d(mv_x)}/{dt} = m{dv_x}/{dt}= ρ{dv_x}/{dt}dxdydz$$ $$F_{g,x} = ρg_xdxdydz$$ De kracht ten gevolge van drukverschillen in de x-richting kunnen we als volgt schrijven (want $F = p·A$):
$$F_{p,x} = [p]_xdydz - [p]_{x+dx}dydz = ([p]_x-[p]_{x+dx})dydz$$ (Hierin betekent de notatie $[Y]_x$ "de waarde van variabele $Y$ op plaats $x$".)
Voor $F_{s,x}$ kijken we naar de schuifspanning die door snelheidsgradiënten op de zijwanden van de kubus optreedt. Het fluïdum dat zich onder de kubus bevindt, oefent in de x-richting een kracht $[τ_{zx}dxdy]_z$ uit op de kubus. Op het bovenvlak geldt, dat $[τ_{zx}dxdy]_{z+dz}$ de kracht voorstelt die het fluïdum in de kubus uitoefent op het fluïdum erboven, dus als we de kracht willen weten die het fluïdum boven de kubus uitoefent op het fluïdum in de kubus, moeten we daar volgens Newton een minteken voor zetten: $-[τ_{zx}dxdy]_{z+dz}$. Voor het boven- en ondervlak samen geldt dus:
$$[τ_{zx}dxdy]_z-[τ_{zx}dxdy]_{z+dz} = ([τ_{zx}]_z-[τ_{zx}]_{z+dz})dxdy$$ Op dezelfde manier kunnen we voor het linker- en rechtervlak en voor het voor- en achtervlak schrijven:
$$([τ_{xx}]_x-[τ_{xx}]_{x+dx})dydz$$ $$([τ_{yx}]_y-[τ_{yx}]_{y+dy})dxdz$$ waarmee de gehele formule wordt:
$$ρ{dv_x}/{dt}dxdydz = Φ_{p,x,in} - Φ_{p,x,uit} + ([τ_{xx}]_x-[τ_{xx}]_{x+dx})dydz +([τ_{yx}]_y-[τ_{yx}]_{y+dy})dxdz +([τ_{zx}]_z-[τ_{zx}]_{z+dz})dxdy + ([p]_x-[p]_{x+dx})dydz + ρg_xdxdydz$$ We zien in de meeste termen combinaties van dx, dy en dz terugkomen. We kunnen de formule vereenvoudigen door te delen door dxdydz:
$$ρ{dv_x}/{dt} = {Φ_{p,x,in} - Φ_{p,x,uit}}/{dxdydz} +{[τ_{xx}]_x-[τ_{xx}]_{x+dx}}/{dx} +{[τ_{yx}]_y-[τ_{yx}]_{y+dy}}/{dy} +{[τ_{zx}]_z-[τ_{zx}]_{z+dz}}/{dz} + {[p]_x-[p]_{x+dx}}/{dx} + ρg_x$$ Op vier plaatsen zien we termen van de vorm ${f(x)-f(x+dx)}/{dx}$. In deze vorm herkennen we de negatieve afgeleide van de functie f(x), want $f'(x) ={f(x+dx)-f(x)}/{dx}$. Zo kunnen we dus schrijven:
$$ρ{∂v_x}/{∂t} = {Φ_{p,x,in} - Φ_{p,x,uit}}/{dxdydz} -{∂τ_{xx}}/{∂x} -{∂τ_{yx}}/{∂y} -{∂τ_{zx}}/{∂z} - {∂p}/{∂x} + ρg_x$$ (Hierin zijn de d's in de afgeleiden vervangen door kromme d's om aan te geven dat het hier steeds partiële afgeleiden betreft.)
Voor de eerste twee termen aan de rechterkant van de oorspronkelijke formule, $Φ_{p_x, in} - Φ_{p,x,uit}$, bekijken we de impuls in de x-richting die met het fluïdum mee de kubus instroomt bij de zes buitenvlakken.
Voor het linker zijvlak geldt: $Φ_{p,x,in} = Φ_mv_x = ρv_xAv_x = ρv_xdydz v_x$. Op dezelfde manier als bij de andere termen, kunnen we deze herschrijven door te delen door dxdydz. Zo wordt de impulsbalans:
$$ρ{∂v_x}/{∂t} = -ρv_x{∂v_x}/{∂x}-ρv_y{∂v_x}/{∂y}-ρv_z{∂v_x}/{∂z} -{∂τ_{xx}}/{∂x} -{∂τ_{yx}}/{∂y} -{∂τ_{zx}}/{∂z} - {∂p}/{∂x} + ρg_x$$ waarmee we de uiteindelijke vorm krijgen:
$$ρ ( {∂v_x/∂t} + v_x{∂v_x/∂x} + v_y{∂v_x/∂y} + v_z{∂v_x/∂z} ) = - ( ∂τ_{xx}/∂x + ∂τ_{yx}/∂y + ∂τ_{zx}/∂z ) - ∂p/∂x + ρg_x$$ Voor de y- en de z-richting kunnen we overeenkomstige vergelijkingen afleiden.
Deze vergelijkingen zijn varianten van de Navier-Stokes-vergelijkingenw. De vorm hierboven is, in tegenstelling tot de Navier-Stokes-vergelijkingen, ook geldig voor niet-newtonse vloeistoffen.
Zie ook
Macroscopische impulsbalansVraagstukken
Termen
Leg van ieder van de gekleurde onderdelen in onderstaande formule uit wat de betekenis ervan is.
Hellend vlak
Een laagje water van 1,0 mm ligt op een plat vlak dat een hoek van 1,0° met de horizontaal maakt.a. Leid uit een impulsbalans af hoeveel de snelheid van het vrije oppervlak bedraagt.
b. Verwacht je dat de stroming in het laagje laminair is, of turbulent?
⬇ hint (a)
Impulsbalans voor de x-richting, met de x-as op het oppervlak in de stroomrichting en de z-as loodrecht op het wateroppervlak.
⬇ antwoord (a)
We gaan uit van
$ρ ( {∂v_x/∂t} + v_x{∂v_x/∂x} + v_y{∂v_x/∂y} + v_z{∂v_x/∂z} ) = - ( ∂τ_{xx}/∂x + ∂τ_{yx}/∂y + ∂τ_{zx}/∂z ) - ∂p/∂x + ρg_x$
en brengen deze vergelijking met de juiste argumentatie (stationair; termen met afgeleiden naar $x$ en $y$ zijn nul; $v_y$ en $v_z$ zijn nul) terug tot:
$ρ ( 0 + 0 + 0 + 0 ) = - ( 0 + 0 + ∂τ_{zx}/∂z ) - 0 + ρg_x$
ofwel: $∂τ_{zx}/∂z = ρg\s\i\n(α)$ (met $α$ de hoek van het vlak met de horizontaal).
Hieruit volgt: $τ_{zx} = ρg\s\i\n(α)z + C_{int}$, en met $τ_{zx}=0$ op het vrije oppervlak (dus $C_{int}=0$) volgt: $τ_{zx} = ρg\s\i\n(α)z$, en omdat het over water gaat, geldt dus: $-μ∂v_x/∂z = ρg\s\i\n(α)z$.
Nog eens integreren naar $z$: $v_x = -{ρg}/{2μ}\s\i\n(α)z^2 + C_2$.
Nu geldt: $v(d) = 0$, waaruit volgt: $v_x = {ρg}/{2μ}\s\i\n(α)(d^2 - z^2)$.
$ρ ( {∂v_x/∂t} + v_x{∂v_x/∂x} + v_y{∂v_x/∂y} + v_z{∂v_x/∂z} ) = - ( ∂τ_{xx}/∂x + ∂τ_{yx}/∂y + ∂τ_{zx}/∂z ) - ∂p/∂x + ρg_x$
en brengen deze vergelijking met de juiste argumentatie (stationair; termen met afgeleiden naar $x$ en $y$ zijn nul; $v_y$ en $v_z$ zijn nul) terug tot:
$ρ ( 0 + 0 + 0 + 0 ) = - ( 0 + 0 + ∂τ_{zx}/∂z ) - 0 + ρg_x$
ofwel: $∂τ_{zx}/∂z = ρg\s\i\n(α)$ (met $α$ de hoek van het vlak met de horizontaal).
Hieruit volgt: $τ_{zx} = ρg\s\i\n(α)z + C_{int}$, en met $τ_{zx}=0$ op het vrije oppervlak (dus $C_{int}=0$) volgt: $τ_{zx} = ρg\s\i\n(α)z$, en omdat het over water gaat, geldt dus: $-μ∂v_x/∂z = ρg\s\i\n(α)z$.
Nog eens integreren naar $z$: $v_x = -{ρg}/{2μ}\s\i\n(α)z^2 + C_2$.
Nu geldt: $v(d) = 0$, waaruit volgt: $v_x = {ρg}/{2μ}\s\i\n(α)(d^2 - z^2)$.
⬇ antwoord (b)
De maximale snelheid is ${ρg}/{2μ}\s\i\n(α)d^2$ = 8,6 cm/s, dus $Re = 86$, dus dat zal nog wel laminair zijn. Maar doordat de laagdikte in het kwadraat in de snelheid zit en er in $Re$ nóg een keer in komt, wordt een laagje al snel turbulent als het dikker wordt.
Laatste wijziging: 26-10-2023
Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.
Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.
