Instationair stoftransport

De differentiaalvergelijkingen (balansvergelijking, transportvergelijking) die gelden voor instationair stoftransport lijken heel erg op die voor instationair warmtetransport. Het is dan ook niet gek dat de oplossingen ervan voor veel situaties ook heel erg op die voor warmtetransport lijken.

Het enige waar we goed op moeten letten, zijn de randvoorwaarden die we gebruiken. Bij warmtetransport is de grootheid die we gebruiken continu in de plaats: de functie vertoont geen sprongen. We hebben gezien dat dit bij stofoverdracht anders is.

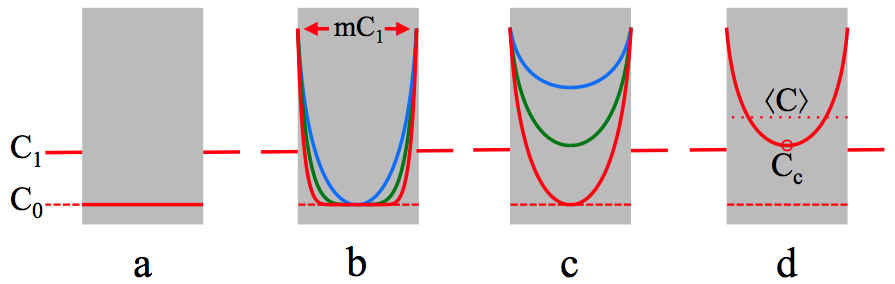
In figuur 1 zien we wat dat betekent: de concentratie van stof X is links van het grensvlak (in stof A) niet gelijk aan rechts van het grensvlak (in stof B). Wanneer in evenwicht geldt dat de concentratie van stof X in stof B m (de verdelingsconstante) keer de concentratie in stof A is, wordt de concentratie in stof B op de grens met stof A gelijk aan $mC_2$ als de concentratie erbuiten $C_2$ is.

Zoals bij opwarming, kunnen we hier spreken van een indringdiepte, waarbij de diffusiecoëfficiënt D de plaats van de warmtevereffeningscoëfficiënt a inneemt:
$$x_i = √{πDt}$$

Figuur 1. Indringdiepte.

Figuur 2 laat diffusie van beide kanten zien. Hiervoor kunnen we dezelfde figuren gebruiken als opwarming (of afkoeling) van twee kanten: de Fourier-grafieken op TPDC-91+92, met:
$${Fo} = {Dt}/d^2$$ $$M = {C – C_1}/{C_0 – C_1}$$
Daarbij moeten we, zoals al gezegd, goed opletten dat we voor de concentratie aan de rand de concentratie binnen het voorwerp nemen.

Figuur 2. Indringing van stof van twee kanten.

De simulaties van eenzijdige indringing^w, tweezijdige indringing^w en tweezijdig wegstromen^w die bij instationaire warmteoverdracht stonden, kunnen dus ook gebruikt worden om het diffusieproces te illustreren.

Opmerking 1: De verdelingscoëfficiënt m kan ook andersom gedefinieerd zijn (namelijk als de concentratie buiten het voorwerp gedeeld door die binnen het voorwerp in evenwicht). In dat geval moet uiteraard juist door m gedeeld worden om de concentratie aan de binnenkant te krijgen.

Opmerking 2: Een bijzonder geval is het als we mogen aannemen dat de concentratie buiten het voorwerp verwaarloosbaar klein is. In dat geval is de concentratie binnen het voorwerp natuurlijk ook nul, onafhankelijk van de waarde van m.

Opmerking 3: Analoog aan de situatie bij warmteoverdracht is de voorwaarde om de Fourier-grafiek te mogen toepassen dat de concentratie op de rand van het voorwerp constant moet zijn.

Vraagstukken

Cilinder

Een lange kunststof cilinder (diameter $d$ = 1,0 cm) bevat een weekmaker die in de kunststof een diffusiecoëfficiënt $D$ van 0,20·10^-9 m²/s heeft. De uniforme beginconcentratie van de weekmaker is $C_0$. De cilinder staat in een oplosmiddel waarin de concentratie van de weekmaker verwaarloosbaar is.
a. Na hoelang is de gemiddelde concentratie van de weekmaker in de cilinder 0,10·$C_0$?
b. Wat is op dat moment de concentratie op de as van de cilinder, uitgedrukt in $C_0$?

⬇ hint (a)

Fouriergrafiek toepassen. Concentratie buiten is nul, dus evenwichtsconcentratie binnen is ook nul.

⬇ antwoord (a)

$⟨M⟩ = {0 - 0,1C_0} / {0 - C_0} = 0,1$ ⇒ $Fo = 0,085$ ⇒ $t = 0,085 d^2/D$ = 4,25·10⁴ s = 12 uur.

⬇ antwoord (b)

$Fo$ nog steeds 0,085 ⇒ $M_c$ = 0,2 ⇒ $C_c = 0,2C_0$.

Gips

Op een laagje gips (calciumsulfaat) in een bakje wordt een laagje schoon water gegoten van 5,0 cm diep. De verzadigingsconcentratie van het gips in water is 2,4 kg/m³. Hoelang duurt het, voordat aan het wateroppervlak de concentratie 2,0 kg/m³ is?

⬇ hint

Modelleer het laagje water (waarin éénzijdige diffusie optreedt met isolatie aan de bovenkant) als een twee keer zo dikke laag (met tweezijdige diffusie) en gebruik de Fourier-grafiek voor centrumconcentratie. Schat de diffusiecoëfficiënt op basis van die van $\C\a^{2+}$ en $\S\O_4^{2-}$.

⬇ antwoord

De diffusiecoëfficiënt van de calcium- en de sulfaationen in water bedraagt ongeveer 1,0·10^-9 m²/s (0,8·10^-9 m²/s voor $\C\a^{2+}$ en 1,1·10^-9 m²/s voor $\S\O_4^{2-}$ ⇒ “gemiddeld” 1,0·10^-9 m²/s).
$M_c = {C_1 - C} / {C_1 - C_0} = {2,4 - 2,0} / {2,4 - 0} = 0,17$ ⇒ $Fo$ = 0,2. Met de geschatte $D$ en $x$ = 0,1 m (twéé keer de laagdikte!) volgt $t$ = 2·10⁶ s = 23 dagen.

Regendruppel

Een vallende regendruppel (diameter $d$ = 2,0 mm) bevat op tijdstip t = 0 geen stikstofoxide, maar valt daarna door lucht die wel stikstofoxide bevat. De N₂O-concentratie in het water aan het oppervlak wordt daardoor 1,0 g/L.
a. Na hoeveel tijd is de N₂O-concentratie in het centrum van de druppel gestegen tot 0,9 g/L, als we aannemen dat de weerstand tegen stofoverdracht geheel in de druppel ligt?
b. Hoeveel stikstofoxide is er op dat moment in de druppel aanwezig?
c. Als de druppel een diameter van 1,0 mm gehad zou hebben, hoeveel stikstofoxide zou er op dat moment in de druppel aanwezig zijn op het moment dat de concentratie in het middelpunt 0,9 g/L bedraagt?

⬇ antwoord (a)

$M_c = {1 - 0,9} / {1 - 0} = 0,1$ ⇒ $Fo$ = 0,075 ⇒ $t$ = 142,9 s = 2,4 min.

⬇ hint (b)

Gebruik de gemiddelde concentratie.

⬇ antwoord (b)

$Fo$ = 0,075 ⇒ $⟨M⟩$ = 3·10^-2 ⇒ $⟨C⟩$ = 0,97 g/L. Met $V = π/6 d^3$: $m = ⟨C⟩·V$ = 4,0·10^-9 kg.

⬇ antwoord (c)

Zelfde $Fo$ ⇒ zelfde $⟨C⟩$. Vanwege $d^3$-verhouding: een achtste van de hoeveelheid stof (en dit duurt ook veel korter, natuurlijk).

Viltstifttekst

Op een skippybal is een tekst aangebracht met viltstift. De lijnbreedte is direct na het aanbrengen 1,0 mm. Na een jaar blijkt de lijn vager te zijn geworden en ongeveer twee keer zo breed. Maak een schatting van de diffusiecoëfficiënt van de inkt in het plastic van de bal.

⬇ hint

Indringdiepte: aan iedere kant 0,5 mm.

⬇ antwoord

$x_i = √{π·D·t}$ ⇒ met 0,5 mm en gegeven $t$: $D$ = 2,5·10^-15 = 3·10^-15 m²/s

Tentamenvraagstukken

Benzeen (1) - Druppel - Ethyn, a.k.a. acetyleen - Microcapsules - N₂ & O₂ (1) - Solvine

Laatste wijziging: 12-10-2022

Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.