Warmtetransport
Warmte kan op drie manieren getransporteerd worden:
• geleiding: transport door een stilstaande stof;
• convectie: transport door meevoering met een bewegende stof;
• stralingw: transport waar geen stof bij nodig is - dit valt buiten de inhoud van deze module.
Geleiding
Wanneer een voorwerp aan één kant warmer is dan aan de andere kant, bewegen de moleculen in het warme deel sneller dan in het koudere deel. Door overdracht van kinetische energie bij botsingen wordt de energie (warmte) van de warme naar de koude kant getransporteerd. Als de warmte niet aangevuld wordt, koelt de warme kant af en warmt de koude kant op, totdat een homogene temperatuur bereikt is. Wordt de warmte wel aangevuld en blijft de koude kant koud (zoals bij een raam tussen een warme kamer en een koude winterlucht), dan zal er een continu warmtetransport door het voorwerp zijn.
De transportvergelijking voor warmte ($q$) luidt in dit geval (zie ook transportvergelijkingen):
$$φ_{q,x} = -λ {dT}/{dx}$$ Deze vergelijking wordt de wet van Fourier genoemd.
Hierin is $λ$ de warmtegeleidingscoëfficiënt.
Voor de totale warmtestroom door een oppervlak A geldt dan:
$$Φ_{q,x} = A·φ_{q,x} = -Aλ {dT}/{dx}$$
Als het binnenoppervlak van een raam dezelfde temperatuur zou hebben als de lucht in de kamer, en het buitenoppervlak de temperatuur van de buitenlucht, zou de warmtestroom alleen bepaald worden door het temperatuurverschil $ΔT=T_1-T_2$, de dikte van het glas $D$ en de warmtegeleidingscoëfficiënt $λ$ ervan. Zie figuur 1 (a) hieronder, waarin de temperatuur als functie van de plaats is getekend.
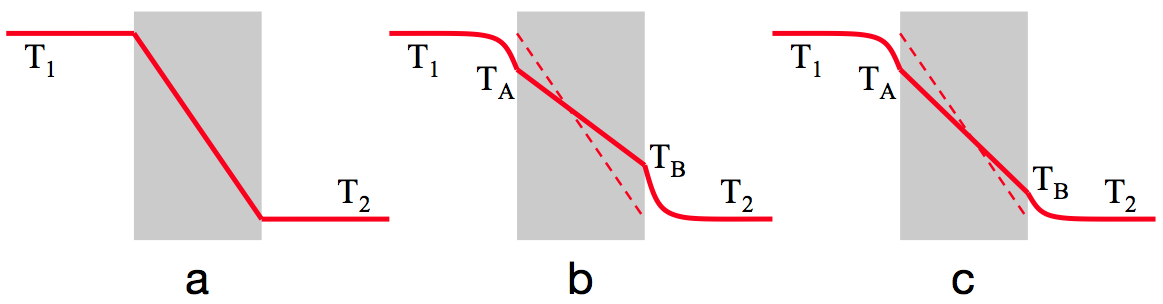
Figuur 1. Temperatuur rond een raam: $T_1$ en $T_2$ zijn de binnen- en de buitentemperatuur.
(a) met constante temperatuur aan de randen; (b) met warmteoverdrachtscoëfficiënt; (c) met hogere warmteoverdrachtscoëfficiënt.
Voor de warmteoverdracht geldt dan, absoluut gezien:
$$Φ_q = A·φ_{q,x} = Aλ {dT}/{dx} = Aλ {ΔT}/D$$
Convectie
In werkelijkheid zal de lucht aan de binnenkant van het raam wat afgekoeld worden (naar $T_A$) – zie figuur 1 (b) – en aan de buitenkant opgewarmd ($T_B$). Daardoor wordt de temperatuurgradiënt in het glas lager. Aan de binnenkant en aan de buitenkant is er een weerstand tegen warmteoverdracht bijgekomen, die wordt bepaald door de snelheid waarmee de warmte door de lucht wordt afgevoerd. Dit meevoeren van warmte door een fluïdum heet convectie.
De convectie wordt uitgedrukt door de warmteoverdrachtscoëfficiënt, $h$. Hoe groter de warmteoverdracht, des te hoger is zal $h$ zijn. Als bijvoorbeeld de wind sterker wordt, wordt $h_2$ hoger, en zal de $T_B$ dalen – zie tekening (c). Voor de luchtlaag aan de binnenkant geldt:
$$Φ_q = A·h_1·(T_1-T_A)$$ Aan de buitenkant geldt:
$$Φ_q = A·h_2·(T_B-T_2)$$ Bovendien weten we voor het glas:
$$Φ_q = Aλ/D (T_A-T_B)$$
Omdat de drie warmtestromen aan elkaar gelijk zijn (het is dezelfde warmte die van binnen naar buiten stroomt), kunnen we de vergelijkingen samenvoegen en omwerken tot de volgende vergelijking:
$$Φ_q = A·1/{1/h_1+D/λ+1/h_2}(T_1-T_2)$$ We kunnen nu een totale warmteoverdrachtscoëfficiënt $U$ invoeren, waarvoor geldt:
$$U = 1/{1/h_1+D/λ+1/h_2}$$ zodat:
$$Φ_q = A·U·ΔT$$ Zijn er meer lagen, zoals bij dubbel glas of een reactorvat met een isolatielaag om de vatwand, dan geldt algemeen:
$$U = 1/{∑↙{i} {1/h_i}+∑↙{j} {D_j/λ_j}$$
In een later college zullen we zien hoe we $h$ kunnen bepalen, maar we kunnen er al wel mee rekenen.
Vraagstukken
Isolatie
Een houten wand met een dikte van 1,0 cm en een warmtegeleidingscoëfficiënt van 0,2 W/(m·K) wordt voorzien van een isolatielaag (λ = 0,02 W/(m·K)) van 0,50 cm dik.a. Hoeveel bedraagt de warmtestroom door de twee lagen als de temperatuur aan de buitenzijde van het hout 20 °C is en aan de buitenzijde van de isolatie 10 °C?
b. Hoe hoog is dan de temperatuur op de grens tussen hout en isolatie?
c. Als bekend is dat de warmteoverdrachtscoëfficiënt aan iedere zijde van de wand 10 W/(m²K) is, hoeveel bedraagt dan de warmtestroom door de lagen bij een totaal temperatuurverschil van 10 °C?
⬇ antwoord (a)
$1/U = x_1/λ_1 + x_2/λ_2 = {0,01}/{0,2} + {0,005}/{0,02} = 0,3$ ${\m^2\K}/\W ⇒ U = 3,33$ $\W/{\m^2\K} ⇒ φ_q = U·ΔT = 33$ $\W/\m^2$
⬇ antwoord (b)
Voor de houtlaag geldt: $ΔT = φ_qd/λ = {33,3}·{0,01}/{0,2} = 1,667$ $°\C ⇒ T_{tussen} = 20 - 1,667 = 18,3$ $°\C$
⬇ antwoord (c)
$1/U = x_1/λ_1 + x_2/λ_2 + 1/h+1/h = {0,01}/{0,2} + {0,005}/{0,02} + 1/{10} +1/{10} = 0,5$ ${\m^2\K}/\W ⇒ φ_q = U·ΔT = 20$ $\W/\m^2$
Collegezaal
In een collegezaal (volume 1,0·104 m³) bevinden zich duizend studenten. De temperatuur in de zaal wordt bepaald door:• de warmte die door de aanwezigen wordt geproduceerd (100 W per persoon);
• de buitenlucht ($T_0$ = 16°C) die de zaal in wordt geblazen (10 m³/s);
• warmteverliezen door het glas van de ramen.
De ramen hebben een oppervlak van 100 m2, een dikte van 5,0 mm en een warmtegeleidingscoëfficiënt van 0,90 W/(m·K). Aan de binnen- en aan de buitenzijde is de warmteoverdrachtscoëfficiënt 10 W/m²K.
a. Wat is de totale warmteoverdrachtscoëfficiënt van de ramen?
b. Bepaal hoe hoog uiteindelijk (in de stationaire toestand) de temperatuur in de zaal wordt.
Op het moment dat de temperatuur in de zaal 23°C is, verlaat iedereen de zaal voor een pauze van 15 minuten.
c. Wat is de temperatuur in de zaal als de studenten weer terugkomen?
⬇ hint (a)
Met formule voor samenstellen van warmteweerstanden.
⬇ antwoord (a)
$1/U = d/λ + 1/h_{binnen} + 1/h_{buiten}$ ⇒ $U = 4,86$ $\W/(\m^2\K)$
⬇ hint (b)
Stationaire situatie: ${dq}/{dt} = 0$.
⬇ antwoord (b)
${dq}/{dt} = UA(T_0 - T) + ρc_pΦ_v(T_0 - T) + N·P$ = 0 (stationair) ⇒ $T_0 - T = -8$ $°\C ⇒ T = 24$ $°\C$
⬇ hint (c)
Oplossen van de DV.
⬇ antwoord (c)
${dq}/{dt} = ρc_pV{dT}/{dt} = UA(T_0 - T) + ρc_pΦ_v(T_0 - T) = (UA + ρc_pΦ_v) (T_0 - T)$ ⇒ ${dT}/{T_0 - T} = {UA + ρc_pΦ_v}/{ρc_pV} dt$
integreren: $T_{eind} = 18,7$ $°\C$
integreren: $T_{eind} = 18,7$ $°\C$
Tentamenvraagstukken
Deksel - Geleiding vs stroming - Glycerol (1)Laatste wijziging: 11-10-2024

Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.

Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.
