Rankine-kringloop
De ideale Carnot-cyclus wordt in de praktijk benaderd door de Rankine-cyclus. Hierbij is o.a. de isotherme warmtetoevoer van de Carnot-cyclus vervangen door isobare verhitting inclusief faseovergang en de isotherme warmteafvoer vindt plaats door middel van condensatie. De stoomcyclus bij elektriciteitsproductie is een uitvoeringsvorm van de Rankine-cyclus.
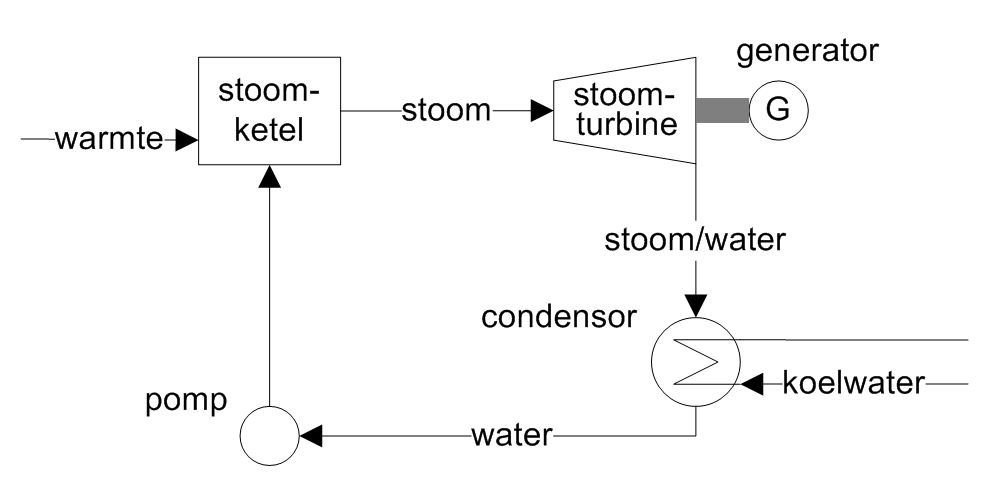
Een stoomcyclus (zie onderstaande figuur) bestaat in grote lijnen uit de volgende stappen (en onderdelen):
• in een stoomketel wordt verbrandingswarmte gebruikt om water via een aantal stappen om te zetten in oververhitte stoom
• deze stoom gaat naar een stoomturbine die gekoppeld is aan een generator, in de stoomturbine expandeert de stoom tot oververzadigde stoom waardoor een deel van de stoom condenseert
• het stoom/water-mengsel wordt verder gecondenseerd tot water in de condensor
• een pomp brengt het water weer op de oorspronkelijke druk
Gesteld dat de temperatuur van de stoom 415 °C is en van het koelwater 15 °C. Dan komt het Carnot-rendement, het theoretisch maximaal haalbare rendement, van de stoomcyclus uit op 58 procent. Onderstaande figuur laat het T,S-diagram van een eenvoudige, ideale Rankine-cyclus zien. De (voedingswater)pomp bevindt zich tussen de punten 1 en 2, de stoomketel tussen de punten 2 en 3, de stoomturbine tussen de punten 3 en 4 en de condensor tussen de punten 4 en 1.
Het rendement van een Rankine-cyclus is de hoeveelheid arbeid die netto geproduceerd wordt, dat wil zeggen de hoeveelheid arbeid die de turbine levert minus de benodigde arbeid benodigd voor compressie, gedeeld door de hoeveelheid warmte die toegevoerd wordt bij het verwarmen, verdampen en oververhitten van water tot stoom. In formulevorm:
$$ η = W_\net / Q_\in $$
Uitgaande van de punten in bovenstaande figuur is het rendement van deze cyclus inclusief oververhitting gelijk aan:
$$ η = {W_{\3->4} + W_{\1->2}} / Q_{\2->3} $$
en met toepassing van de eerste hoofdwet(*), wordt dit:
$$ η = {(H_3 - H_4) + (H_1 - H_2)} / {(H_3 - H_2)} $$
Bovenstaande vergelijking kan desgewenst worden omgeschreven tot:
$$ η = {|H_3 - H_4| - |H_1 - H_2|} / {|H_3 - H_2|} $$
Het rendement van een Rankine-cyclus kan verhoogd worden door de stoom te heroververhitten. Het bijbehorende T,S-diagram is te vinden in onderstaande figuur, waarbij tussen de punten a en b de heroververhitting plaatsvindt.
Uitgaande van de punten in bovenstaande figuur wordt het rendement nu:
$$ η = {(H_3 - H_a) + (H_b - H_c) + (H_1 - H_2)} / {(H_3 - H_2) + (H_b - H_a)} $$
of, anders opgeschreven:
$$ η = {|H_3 - H_a| + |H_b - H_c| - |H_1 - H_2|} / {|H_3 - H_2| + |H_b - H_a|} $$
Een andere manier om het rendement verhogen is het toepassen van een voedingswatervoorverwarmer en leidt tot onderstaand T,S-diagram. Hiervoor wordt een deel van de stoom voortijdig afgetapt bij de stoomturbine (punt a), gemengd(**) met water uit de voedingswaterpomp (punt c), verder op druk gebracht en tussen de punten (d) en (3) in een boiler verhit tot oververhitte stoom. De warmte benodigd voor het opwarmen tussen de punten (b) en (c) is afkomstig van de afgetapte stoom. Het bijbehorende schema is evt. hierw te bekijken. Combinaties van heroververhitters en voedingswatervoorverwarmers zijn uiteraard ook mogelijk.
Op basis van de punten in bovenstaande figuur geldt voor het rendement nu (turbine-arbeid wordt in twee delen berekend vanwege de aftapstroom):
$$ η = {(H_3 - H_a) + (H_a - H_4) + (H_1 - H_b) + (H_c - H_d)} / {(H_3 - H_d)} $$
of, anders opgeschreven:
$$ η = {|H_3 - H_a| + |H_a - H_4| - |H_1 - H_b| - |H_c - H_d|} / {|H_3 - H_d|} $$
(*) Voor turbines en pompen geldt dat de kinetische en potentiële energietermen evenals de uitwisseling van warmte met de omgeving verwaarloosd kunnen worden.
(**) Indien een open voedingswatervoorverwarmer wordt toegepast. Bij een gesloten voedingswatervoorverwarmer wordt warmte overgedragen dmv een warmtewisselaar en vindt menging plaats na drukverhoging tot de druk van het voedingswater.
Achtergrondinformatie
• Rankine-kringloopw (standaard- en werkelijke kringloop plus verbeteringen)
Laatste wijziging: 21-10-2024

Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.

Deze publicatie valt onder een Creative Commons licentie. Zie hiervoor het colofon.