Numerieke methoden

In deze module maken we vooral gebruik van methoden die ontwikkeld zijn vóór de opkomst van de computer in dit vakgebied. Met deze methoden kunnen we voor veel situaties realistische berekeningen uitvoeren, en ze geven ook inzicht in en gevoel voor de processen die optreden.

Wanneer de systemen complexer worden, gelden de voorwaarden waaronder deze methoden mogen worden toegepast meestal niet meer. Sinds de komst van de computer zijn op alle deelgebieden van het vakgebied de toepassingsmogelijkheden en het inzicht in de processen enorm toegenomen.

We zullen hier twee eenvoudige voorbeelden bekijken van hoe de modelvergelijkingen kunnen worden vertaald naar een numeriek model.

Vallend voorwerp

Met de theorie van deze module kunnen we de kracht berekenen op een voorwerp dat zich met een bepaalde snelheid door een fluïdum beweegt, of de eindsnelheid van een voorwerp dat door een fluïdum valt. Maar hoe snel bereikt zo'n voorwerp die eindsnelheid? Als we dat willen weten, moeten we een dynamisch model maken, waarin de wrijvingskracht op het voorwerp snelheids-, en dus tijdsafhankelijk is.

Voor de totale kracht $F_{tot}$ op zo'n voorwerp geldt op ieder moment:

$$F_{tot} = F_g + F_A + F_d$$
waarin $F_g$ de zwaartekracht is (= $-m·g$), $F_A$ de Archimedeskracht^w, en $F_d$ de weerstandskracht. Daarnaast weten we dat deze totale kracht evenredig is met de versnelling van het voorwerp:

$$F_{tot} = m·a$$
Zo kunnen we op ieder moment de versnelling bepalen - mits we de weerstandscoëfficiënt weten, natuurlijk, en daarover hebben we tot nu toe alleen informatie in de vorm van een tabel of grafiek in TPDC. Met een relatie in formulevorm kunnen we een numeriek model opstellen. Voor bollen zijn veel formules afgeleid, maar onderstaande formule geeft een redelijke benadering (-4 tot +6%) en is niet al te onhandelbaar (Clift et al., 1978):

$$C_d = {24}/{Re} + {3,6}/{Re^{0,313}}+{0,42}/{1+42500Re^{-1,16}}$$
Bovenstaande formules kunnen we gebruiken in de volgende differentievergelijkingen:

$${∆v}/{∆t} = {F_{tot}/m}$$ $${∆s}/{∆t} = ∆v$$
Wanneer een voorwerp door een vloeistof valt (of erin opstijgt), moet ook een deel van de vloeistof verplaatst en dus versneld worden, waardoor de versnelling bij dezelfde kracht lager is. Voor een bol geldt dan dat voor het berekenen van de versnelling een virtuele massa gebruikt moet worden (zie ook Wikipedia^w):

$$m_{virt} = ρ_{bol}·V + ρ_{fluïdum}·V/2$$
Het is dus eigenlijk alsof een volume van het fluïdum gelijk aan de helft van het volume van de bol mee-versneld moet worden.

Opwarming van een plaat

Wanneer een vlakke plaat aan veranderende temperaturen aan de beide oppervlakken wordt blootgesteld, gaat er warmte stromen. Voor symmetrische situaties (aan beide oppervlakken verandert de temperatuur evenveel) kunnen we inmiddels berekenen hoe de doorwarming verloopt. Als de temperaturen niet symmetrisch verandert, of als de randtemperaturen tijdens het doorwarmingsproces blijven veranderen, kunnen we dat met onze methode niet aan. Dat gaan we hier numeriek benaderen.

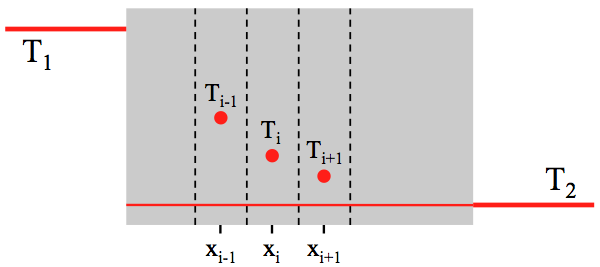
We delen de plaat in dunne plakjes met dikte dx, parallel aan de twee oppervlakken (zie figuur 1).


We gaan er voor de balansvergelijking van uit dat de temperatuur binnen een plakje overal gelijk is. Voor het i-de plakje geldt dan:

$${dq}/{dt} = ρc_pV{dT}/{dt} = ρc_pdx·HB{dT}/{dt} = ∑Φ_q= -λHB({dT}/{dx})_L+λHB({dT}/{dx})_R$$
waarin $H$ de hoogte van de plaat en $B$ de breedte (loodrecht op de tekening) ervan voorstellen, en de subscripts $L$ en $R$ respectievelijk "links" en "rechts". Van deze vergelijking kunnen we de volgende differentievergelijking maken, als we aannemen dat het transport bepaald wordt door het temperatuurverschil tussen de plakjes, werkend over de afstand Δx:

$$ρc_pΔx{ΔT}/{Δt} = -λ{T_{i}-T_{i-1}}/{Δx}+λ{T_{i+1}-T_i}/{Δx} = λ{T_{i-1}-2T_i+T_{i+1}}/{Δx}$$
(in deze vergelijking is meteen HB weggedeeld).
Voor de temperatuurverandering ΔT in een tijdstap Δt krijgen we dus:

$$ΔT = {λ/{ρc_p}} · {T_{i-1}-2T_i+T_{i+1}}/{Δx}^2Δt$$ Deze methode heet de Forward Time, Centered Space (FTCS) methode.
De simulatie waarvan je al eerder voorbeelden zag (bij instationair warmte- en stoftransport), is gemaakt op basis van bovenstaande formule. In de simulatie (klik hier^w) kun je de temperaturen links en rechts én in het midden tijdens de simulatie aanpassen, zodat je het effect meteen kunt zien.

In numerieke simulaties mag de tijdstap niet te groot zijn. De numerieke oplossing van de simulatie hierboven is alleen stabiel als

$${λ}/{ρc_p}Δt < 1/2{Δx}^2$$ Wat er dan gebeurt als dit niet het geval is, kun je hier^w zien. Dit betekent, dat we bij dunnere plakjes (dus voor een in de plaats nauwkeuriger simulatie) de tijdstap kleiner moet maken.

⊕ FTCS?

De FTCS-methode heet zo omdat er gebruik wordt gemaakt van de voorwaartse Euler-methode in de tijd, en van de centrale-differentie-methode in de plaats.

Vraagstukken

Raam

Een kamer waar het 15,0 °C is, heeft een raam met een dikte van 7,0 mm. Buiten is het 10,0 °C. We nemen aan dat de temperatuur van het glas aan beide zijden steeds gelijk is aan de luchttemperatuur daar.
a. Hoeveel bedraagt de temperatuur in het midden van het glas?
De temperatuur in de kamer wordt in korte tijd opgestookt tot 20 °C, waardoor het glas gaat opwarmen. Op een bepaald moment is de temperatuur in het midden van het glas 13,1 °C geworden. De temperaturen op 1,0 mm afstand van het midden zijn 14,4 °C (aan de kamerzijde) en 12,1 °C. Het glas heeft een temperatuurvereffeningscoëfficiënt van 5,0·10^-7 m²/s.
b. Hoe groot mag de tijdstap maximaal zijn als we met deze gegevens volgens bovenstaande methode de temperatuur op de volgende tijdstap willen berekenen?
c. Hoeveel bedraagt de temperatuur in het centrum volgens deze methode na 1,0 s?

Bronnen

Clift et al., 1978, Clift R., Grace J.R. & Weber M.E.; Bubbles, Drops, and Particles, Academic Press, New York

TB241E

Hoofdpagina
College-index
Thematische index
Alles op één pagina
Laatst gewijzigd
Colofon

Op deze pagina: